Basic HTML Version
672
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 5
Punching strength of reinforced concrete flat slabs without shear reinforcement
trend of unsafe results would be modifying the coefficient 0.18 in Equa-
tion 3 to 0.16. This small change would increase the average to 1.14,
same value as CSCT, it wouldn’t change the coefficient of variation, and
what is really important, could reduce the percentage of unsafe results
from 47.3% to 9.5%, leaving the results of this code similar to the CSCT.
7. Conclusions
Several aspects of the development of flat slabs and of the para-
meters that influence their punching resistance were discussed in
this paper. Recommendations of ACI 318 [7], EUROCODE 2 [8]
and NBR 6118 [9] were also presented as well as those from the
Critical Shear Crack Theory , as presented by Muttoni [3], which
is the basis of recommendations for punching presented in new fib
Model Code [4.5]. To evaluate the safety and precision of these
theoretical methods, a database was formed with experimental re-
sults of tests in 74 flat slabs without shear reinforcement.
It was observed that, generally, ACI’s recommendations are meant to be
safe, but underestimate the punching strength of flat slabs in about 37%
for those in the database. This code also presented a high coefficient of
variation (0.16) for this which is the simplest case the design of a slab-
-column connection. EC2 presented satisfactory and safety results, being
registered average results for the ratio
P
u
/
V
calc
of 1.19. This code also
presented a coefficient of variation of 0.14, below of the American code
due to the fact that it takes into account the influence of parameters such
as the flexural reinforcement ratio and size effect, while that the American
code considers only the compressive strength of concrete.
The Critical Shear Crack Theory has been widely discussed by the
scientific community and some critics are noteworthy. The main one,
as pointed out by Ferreira [1], is that according to a scientific point of
view, taking as a fundamental hypothesis that the failure mechanism
by punching occurs with only rigid body rotations of the segment of
slab outside the punching cone (delimited by critical crack) contradicts
experimental evidence (in the region of failure occurs rotation and sli-
ding) and can lead to inappropriate results, especially in the case of
slabs with shear reinforcement (estimating higher forces in the outer
perimeters, which in practice is not observed). From technical point of
view, is a significantly more complex method for routine use in design
offices and, as noted, presents results similar to those from Eurocode.
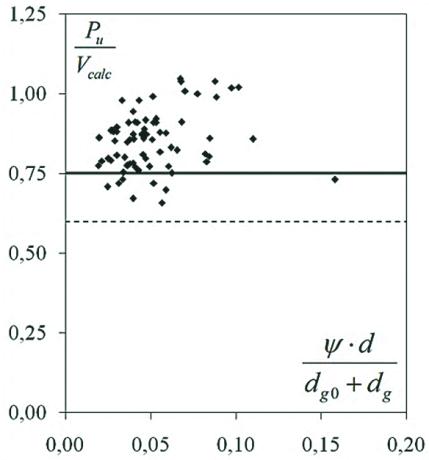
Figure �� � Com�arison of results from database
with those using recommendations of CSCT
Ta�le 2 � Com�arison �et�een e��erimental and theoretical results
Author
d
(mm)
(%)
f
c
(MPa)
P / V
u
calc
ACI
EC2
NB1 CSCT
Aver. COV Aver.
COV Aver.
COV Aver.
COV
Elstner and Hognestad [2]
114�118
1.2 �3.7 20�50 1.42 0.19 1.17 0.11 0.94 0.07 1.02 0.08
Kinnunen and Nylander [14]
117�128
0.8 �1.1 25�28 1.52 0.05 1.19 0.05 1.05 0.06 1.06 0.04
Moe [15]
114 1.1�1.5 20�26 1.47 0.08 1.30 0.05 1.11 0.05 1.14 0.06
Regan [20]
64�200 0.8 �1.5 22�43 1.28 0.11 1.14 0.12 0.93 0.09 1.16 0.11
Marzouk and Hussein [18]
70�120 0.7�2.1 42�80 1.41 0.16 1.39 0.11 1.12 0.09 1.27 0.09
Tomaszewicz [34]
88�275 1.5�2.6 64�119 1.48 0.08 1.11 0.08 1.06 0.07 1.16 0.06
Hallgren [17]
194�202
0.3�1.2 84�109 1.00 0.19 0.94 0.09 0.94 0.08 1.06 0.07
Aver.
1.37
1.19
1.01
1.14
COV
0.16
0.14
0.11
0.11
Min.
0.64
0.78
0.68
0.88
% U.R.
5.4
10.8
47.3
10.8

