Basic HTML Version
607
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 5
V. J. FERRARI | J. B. DE HANAI
gential stress is located at 310 mm from the strengthening end.
For the beam V1C this position was observed at 230 mm from the
strengthening end.
In the beam V1C, the maximum normal stress, 1239 MPa, was
recorded through the strain gauge 18, located at 218 mm from the
section in the middle of span. This value of stress is equivalent
to a deformation in the strengthening equal to 5.30‰. From the
profile of stresses there are the verifications of significant values of
normal stresses (in the order of 450 MPa) and the concentration
of higher values of tangential stresses in the strengthening end at
75% and 100% from the last strength.
In the beam V2C the distribution of normal and tangential stresses
along the strengthening (Figure [14]) indicates maximum values of
1891 MPa and 2 MPa, respectively. The maximum normal stress,
which is equivalent to a strain in the strengthening of 8.08‰, was
recorded by the strain gauge 18 and the maximum tangential
stress was given by the strain gauge 11.
5. Finite element method (FEM) analyses
5.1 Discretization
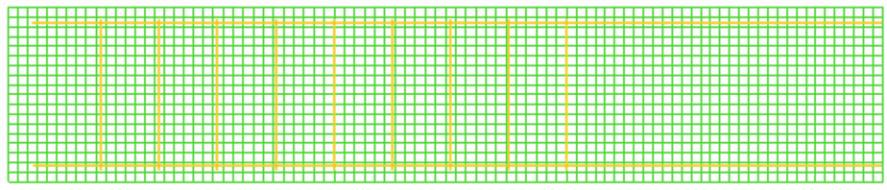
The behaviors of beams V1A, V1C and V2C were nonlinearly
simulated using the computational program of finite elements, Di-
ana version 9.1. In the Figure [15], it is presented the mesh of
two dimensional finite elements along with the arrangement of the
reinforcements in the discretization of the beams. The mesh was
developed using quadratic elements of 8-node type CQ16M. The
longitudinal and transversal bars of the reinforcement of beams
were discretely modeled through special elements called embed-
ded reinforcement.
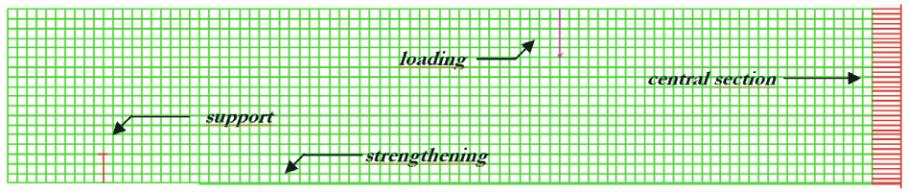
In the Figure [16] it is showed the loading application, the support,
the presence of external strengthening, and the condition of model
symmetry. The bond between the reinforcement and concrete was
considered perfect, eliminating thus the possibility of rupture by
slippage of the bars. The nodes of finite elements, representative
of the external strengthening, were connected with the adjacent
nodes of the concrete elements simulating a perfect bond between
the materials.
The constitutive models of concrete beams considered in the pro-
gram Diana and the mechanical properties of concrete and lower
reinforcement used in the nonlinear analysis of the main beams
V1A, V1C and V2C are listed in the Table [7]. These properties were
obtained through characterization tests described in Ferrari [5].
The values of tensile strength considered for concrete, were those
obtained according to ACI [10] through the equation: 0.332×(f
c
)
1/2
.
The values of crack bandwidth were taken considering the square
root of the finite element area, according to the recommendation
in the Diana [11].
The presence of the transition layer in the beam V2C was estab-
lished through a plane surface located in the tensile zone of the
model. The bond between the transition layer and the surface rep-
resentative of the adjacent concrete was considered perfect. The
mechanical properties of the transition layer of beam V2C were
taken from the characterization values of the cement composite
and are indicated in the Table [8].
The values of tensile strength assumed for the cement composite
were obtained through RILEM TC 162-TDF [8] using the equa-
Figur������������ur�����i�i���������������r���������

