Basic HTML Version
871
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 6
M. N. KATAOKA
| M. A. FERREIRA
| A. L. H. C. EL DEBS
barras de aço de cada modelo. Isso foi possível porque não houve
divergências entre o comportamento das barras. Comparando as
curvas da Figura 14 nota-se a diferença entre o comportamento
de cada ligação, pois para uma mesma intensidade de força a
armadura do Modelo 1 apresentou deformações até 100% maior
em algumas situações. Isso pode ser atribuído ao fato de no Mo-
delo 2 a força ter sido distribuída em um número maior de barras
e possuir laje adjacente, apesar de possuir a mesma área de aço
do Modelo 1.
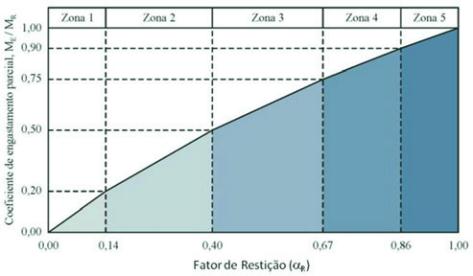
5. Classificação das ligações
Em Ferreira
et al.
[13] é apresentado um sistema de classificação
para ligações no qual elas são subdivididas em cinco zonas distintas,
como mostrado na Figura 15. Esse sistema se baseia no fator de
restrição à rotação (α
R
) (equação 1), um número adimensional que
relaciona a rigidez da ligação à rigidez da viga que nela concorre e
que varia de 0 (articulação perfeita) a 1 (engaste perfeito), e no coe-
ficiente de engastamento parcial (M
E
/M
R
), o qual representa a razão
entre o momento fletor de engastamento parcial e o momento fletor
de engastamento perfeito. Nesse sistema de classificação, a zona 1
corresponde às ligações articuladas, as zonas 2 a 4 correspondem
às ligações semi-rígidas de baixa, média e alta resistência, respecti-
vamente e a zona 5 corresponde às ligações rígidas.
(1)
2
1
sec
sec
.
) (3
1
1
ef
R
LR
EI
Onde:
(EI)
sec
– Rigidez secante da viga conforme a [9]
L
ef
– Vão efetivo entre os apoios, distância entre centros de giros
nos apoios
R
sec
– Rigidez secante ao momento fletor da ligação viga-pilar
θ
1
– Rotação na extremidade da viga
θ
2
– Rotação combinada da extremidade da viga com a da ligação
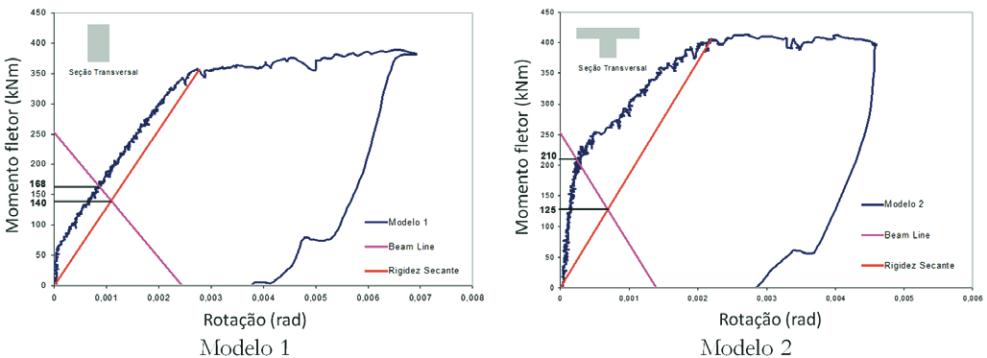
Para a análise da ligação foi utilizado o Método
Beam-Line
, e para isto
foi necessário determinar qual a rotação máxima para uma ligação ar-
ticulada (Figura 17). A análise foi realizada considerando uma viga de
5,8 m de comprimento, com duas forças concentradas de 180 kN, que
no caso de uma ligação rígida geraria um momento coincidente com o
momento último de projeto dos modelos, correspondente a 255 kNm.
Para cada modelo foi considerada uma rigidez de acordo com sua se-
ção transversal, ou seja, para o Modelo 1 seção retangular e para o
Modelo 2 seção “T” com largura colaborante determinada de acordo
com [9], obtendo duas retas Beam-Line respectivamente. Foi calculado
momento de inércia no estádio I e módulo de elasticidade terminado a
partir dos ensaios de caracterização dos corpos de prova. Consideran-
do uma viga bi-apoiada (ver Figura 17) a rotação da viga na região da
extremidade foi calculada de maneira teórica pela equação 2. A Tabela
3 apresenta os valores de rotação para cada modelo com o respectivo
momento de inércia e módulo de elasticidade.
Figura 15 – Sistema de classificação de ligações
proposto por Ferreira et al. (2002) [13]
Figura 16 – Curvas momento fletor
versus
rotação com a indicação da rigidez secante e Beam-Line.

