Basic HTML Version

127
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
R. G. M. de Andrade | L. M. Trautwein | T. N. Bittencourt
detected and hence monitored (Figure 7): S1 and S3, in the
center of spans of 30m and 26m, respectively, S2 and S4, re-
gions right above columns P4 and P5. Sections S1 and S3
presented sagging bending moment and maximum displace-
ments, whereas S2 and S4, high tensile stresses due to hog-
ging bending moment. Thus, it was found that the static vertical
displacement of both girders should be measured by displace-
ment transducers. Still, longitudinal and transverse displace-
ments were monitored by displacement sensors inserted on
the bearing support over columns P4 and P6. Finally, displace-
ment transducers were used to monitor cracks on the outside
face of the girders.
Three accelerometers were installed in regions corresponding to
one of the first vibration modes obtained from Model 4: Sections
S1 and S3.
This paper approaches the results for displacements only. The dy-
namic results and deformations are related to other studies from
monitoring group.
5. Analyses and results
In order to compare the acquired data during bridge monitoring
with numerical models 5 and 6, a previous validation among mod-
els 1 to 5 was carried out.
For convenience, Model 4 was considered master model and was
compared with models 1 to 3. After the comparison among the first
four models, the results regarding vertical displacement was con-
sidered satisfactory [12], enabling the next step which consisted
in validating Model 5. All the vertical displacement comparisons
shown in Table 3 were reliable so the final model could be devel-
oped: Model 6.
It is noticed an error decrease as it moves to the center of the
bigger span. Due to lack of transverse distribution of loading, a
discrepancy between models 1 to 3 and model 4 was expected.
Thus, among the different representations of the structure, the
Model 4 was considered to be satisfactory compared with the
next model, due to a better representation of the bridge struc-
tural behavior of the bridge before the first three models.
Model 5 shows a greater stiffness compared to Model 4, which
resulted in differences in deflection up to 11%. A higher stiffness
was expected due to the stress distribution within the volume
and an increased contribution of the compressed girder flanges.
While modeling Model 5, the prismatic variation of girder width
was possible to be properly done. Thus, Model 5 satisfactorily
represents the structural behaviour and was used as a basis for
generating the model 6.
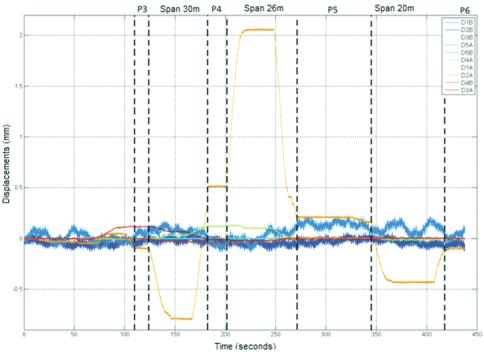
Next, a comparison of the results obtained during monitoring
process will be made, illustrated in Figure 8, with models 5
and 6.
Model 5 required about 10 hours of processing (Intel (R) Core
(TM) i7 CPU 960@3.20GHz, 16BG RAM) for each load case.
Shown in Table 4, the results for the girder at the bigger span
were 17.37% lower than that shown in data acquisition, i.e. it
presented a higher stiffness than the actual structure. The re-
sults for girders A and B at 26m span were, respectively, 10.32%
and 5.39% less than the vertical displacement acquired in mon-
itoring. A suggested f
ck
of 25 MPa was used as a calibration
and convergence response. A reduction of 3.57% in the Elastic
Modulus resulted in an error decrease of 3.40%.
Model 6 required approximately 120 hours of processing for
loadcases located at 30m span, while approximately 40 hours
were required for the loadcases on 26m span. According to
Table 5 for the Elastic Modulus obtained in laboratory, Model 6
showed an error of 21.52% in the girder B, at 30m span, while
girders A and B, at 26m span, were respectively 21.37% and
15.71%. For this model, the calibration was only at energy of
fracture. A decrease of 16.69% in its value led to a vertical dis-
placement reduction of only to 0.73% at 30m span, while other
spans presented no change in displacement. With the decrease
of span length, the energy of fracture had little influence in
changing the results.
6. Conclusions
The refinement of numerical modeling through hierarchy is impor-
tant so the model behaviour and representativeness can increase
and improve. By increasing the number of degrees of freedom of
the numerical model and adding new inherent parameters to the
structure, each step on hierarchy level must provide means of in-
terpretation the results and model calibration, so there is conver-
gence with experimental results. It is also important to emphasize
a deep understanding of each new inserted parameter. The more
complex the model is, the more likely the response will diverge,
compromising the validation of results.
7. Aknowledgements
The authors would like to thank OHL Concession Company for all
logistical support during bridge monitoring over Jaguari river.
Figure 8 – Graphics from acquired data
during monitoring
Girder B
Girder A

