Basic HTML Version

27
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
P. M. LAZZARI | A. CAMPOS FILHO | F. P. S. L. GASTAL | R. A. BARBIERI | R. C. SCHWINGEL
Figure 25 – Placing of the beam
the sum of permanent moment (30% of the total moment) with
variable moment (70% of the total moment), were used as a
calculation artifact to consider the partial incasing of the beam
ends in columns and were obtained by the global analysis of
the structure.
Figure 27 shows the beam’s cross section, consisting of a locally
cast section T, being 50cm high and 75cm wide at the lower foun-
dation and containing passive and active reinforcements. The up-
per compressive flange, belonging to the slab, is 16cm thick and
275cm wide, considering 1 m of slab on each side of the section.
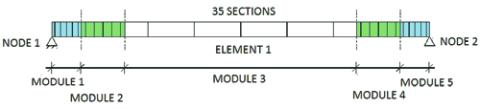
The beam span was modeled using a hybrid single finite element
linked by nodes 1 and 2, as shown in Figure 28. The element was
divided into 35 cross sections distributed in five integration mod-
ules along the element in order to take the location of the passive
reinforcement layers into consideration.
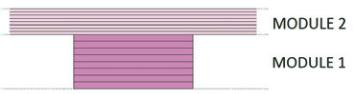
The cross section of the beam was divided into 18 horizontal
planes and in two modules along its height, as shown in Figure 29.
Modules 1 and 2 of the cross section consist of eight layers each.
Layers were 4.25cm and 2cm thick in modules 1 and 2, respec-
tively. As in the previous example, the numerical integration rule of
Gauss-Lobatto was chosen because it is more accurate.
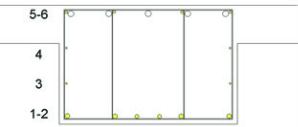
Passive reinforcement tendons were distributed in six layers, as
shown in Figure 30, with a 2.0-cm cover, as determined in the de-
sign. Table 9 presents the characteristics of each passive rein-
forcement layer, including their position, diameter, number of ten-
dons, reinforcement section, and date.
The ten unbonded prestressing tendons present a parabolic pro-
file and are distributed in a single layer, as shown in Figure 31.
Table 10 presents the characteristics of location, diameter, num-
ber of tendons, reinforcement section, and date of active reinforce-
Figure 27 – Beam cross-section(cm)
Figure 28 – F.E. modeding of the beam
Figure 29 – Definition of the
cross-section modules
Figure 30 – Distribution of the passive
reinforcement at the element
and into the cross-section
Figure 26 – Simply supported beam

