Basic HTML Version
98
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 1
Reliability of buildings in service limit state for maximum horizontal displacements
como do aço de reforço. Detalhes dos modelos e da estratégia
de solução do problema não linear são apresentados em CORE-
LHANO [3].
2.3 Análise não-linear física simplificada
A norma ABNT NBR6118:2003 [1] propõe duas alternativas para a
análise não-linear física simplificada de estruturas de concreto ar-
mado. Estes modelos penalizam a rigidez dos membros para levar
em conta, de forma simplificada, os efeitos da fissuração do con-
creto. No primeiro modelo, as rigidezes à flexão de pilares e vigas
são obtidas multiplicando-se os valores referentes à seção bruta
por 0,70. No segundo modelo, as rigidezes equivalentes (fissura-
das) de pilares e vigas são obtidas multiplicando-se as rigidezes
da seção bruta por fatores iguais a 0,80 e 0,40, respectivamente.
Neste trabalho, estes modelos são referenciados como 70/70 e
80/40, respectivamente.
O módulo de elasticidade secante do concreto é estimado como:
(7)
sec
0.85 5600
E
fck
= ×
onde:
E
sec
: módulo de elasticidade secante;
f
ck
: resistência característica do concreto aos 28 dias.
3. Erros de modelo
Os modelos simplificados propostos pela norma ABNT
NBR6118:2003 [1] são, por natureza, aproximados. Uma variável
chamada de Erro de Modelo é obtida dividindo-se os deslocamen-
tos obtidos via análise não-linear física rigorosa pelos desloca-
mentos obtidos via análises simplificadas (OLIVEIRA et al. [9]):
(8)
rigorous
simplifyed
M
u
E
u
=
Trata-se de uma variável aleatória uma vez que, para diferentes
estruturas, o modelo simplificado pode ser mais ou menos preciso.
Uma amostra (conjunto de observações) da variável aleatória erro
de modelo é obtida avaliando-se a equação (8) para diferentes
configurações estruturais.
Neste trabalho, é obtida uma amostra de erro de modelo cor-
respondente a 42 pórticos representativos de estruturas usuais,
variando-se geometria, material e taxa de armadura. São consi-
derados pórticos planos de quatro, oito e doze pavimentos, com
um ou três lances de pilares. A geometria dos pórticos estudados
representa variações dos pórticos apresentados na Figura 3. Fo-
ram considerados concretos com resistências características nas
faixas de 20 a 40 MPa. Quanto às taxas de armadura dos pilares,
os pórticos foram dimensionados em três faixas: baixa, média, e
alta. A taxa de armadura baixa é próxima à armadura mínima; a
média tem taxas da ordem de 2% para os pilares e a taxa de
armadura máxima é equivalente à máxima permitida na ABNT
NBR6118:2003 [1], entre 3 e 4%. Os carregamentos verticais fo-
ram determinados pelo processo das áreas de influência (lajes, vi-
gas, pilares, paredes e revestimentos). O carregamento acidental
foi adotado como 1,5 kN/m² na área de influência. Detalhes das
configurações dos pórticos planos estudados são apresentados
na Tabela 1. Esta tabela também apresenta as observações de
erro de modelo obtidas para cada pórtico.
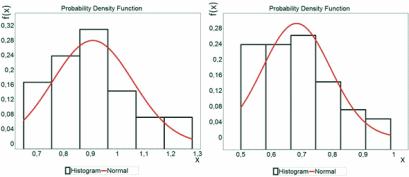
A Figura 4 ilustra os histogramas obtidos com base na amostra
de erros de modelo, bem como as distribuições de probabilidade
ajustadas a estes histogramas. Para o modelo simplificado com
redução de rigidez 70/70 (pilar/viga), obteve-se ajuste a uma dis-
tribuição normal, com parâmetros:
Figura 4 – Histogramas e distribuições de probabilidades para erros de modelo:
redução pilar/viga 70/70 (à esquerda), redução pilar/viga 80/40 (à direita)

