Basic HTML Version
290
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 3
Nanotechnology and Construction: use of nanoindentation measurements to predict macroscale elastic
properties of high strength cementitious composites
3.2 Experimental results in hardened state -
Microscale analysis
3.2.1 Nanoindentation
A total of 288 indents to the cementitious matrix were performed.
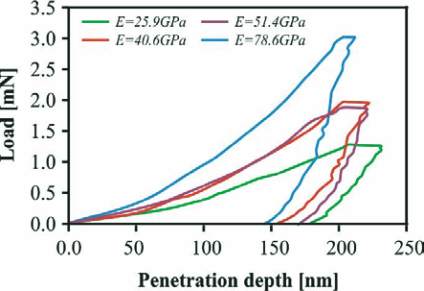
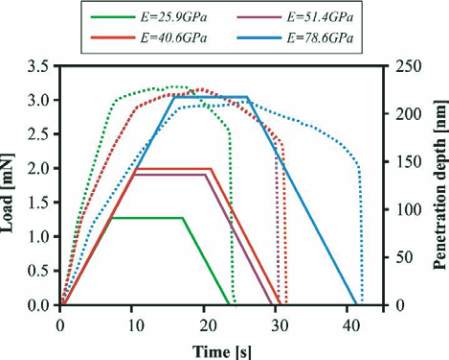
Examples of the load-penetration curves and related load/penetra-
tion-time diagrams showing indents to differently stiff phases are
presented in Figure 5 and 6, respectively.
All relevant indents were analyzed by the Oliver-Pharr method,
[10], for an elastic modulus with the assumption of constant Pois-
son’s ratio 0.2 for all indents, since the influence of the selected
Poisson’s ratio in the relevant range 0.18−0.22 on the evaluation
is very small, [17]. Subsequently, the frequency plots, with bin
size set to 1.0 GPa, and related experimental probability density
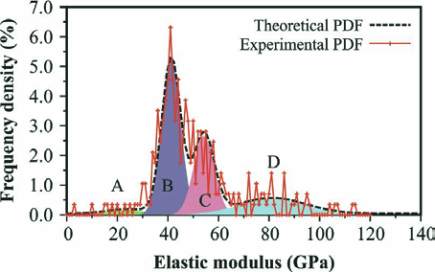
functions (PDFs) were computed. The deconvolution method was
applied to PDFs as illustrated in Figure 7. The obtained results
are listed in Table 6.
As mentioned above, the results are considered as results re-
ceived on mechanically distinct phases and there is no intention
to link them with pure chemical phases, such as C-S-H gels with
different densities, Portlandite, interfacial zones, etc., [5,17,19].
Despite the fact that the results from deconvolution present me-
chanically distinct phases rather than chemically distinct phases,
they are closely related. Based on the SEM imaging, cement
chemistry and mixture composition, it is assumed that the phase
A in Figure 7 is composed of low stiffness porous phases, the
phase B contains majority of the main hydration products (C-S-
H gels and partly Ca(OH)
2
), the phase C is composed of high
stiffness hydration products (high stiffness C-S-H and partly
Ca(OH)
2
), the phase D contains the remaining non-hydrated clin-
ker, fly ash or quartz filler. Due to unavoidable phase interactions,
the obtained elastic moduli do not exactly represent material con-
stants for pure phases, which is manifested mainly for the stiffest
components, such as the clinker, whose elastic modulus reaches
~130 GPa on a pure clinker sample, [25,29]. However, separa-
tion of the mechanical performance of the individual components
is not possible from the measured response and the influence of
Figure 5 – Example of load-penetration curves
Figure 6 – Load and depth
of penetration versus time
Figure 7 – Experimental and best-estimated
PDF obtained by deconvolution
Table 6 – Elastic modulus and volume
fraction obtained by deconvolution
Matrix
phases
Elastic
modulus
[GPa]
S.d.
[GPa]
Volume
fraction
[%]
A
24.4
8.35
6.3
B
41.3
3.70
48.8
C
54.3
4.07
27.4
D
81.2
13.29
17.5

