Basic HTML Version
291
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 3
W. R. L. da Silva | J. Němeček | P. Štemberk
interactions can be just estimated as discussed in section 2.4.1.
Further, the evaluated micromechanical values are considered
as the first estimates and as such they neglect the interaction
phenomena in the following upscaling.
3.2.2 Homogenization
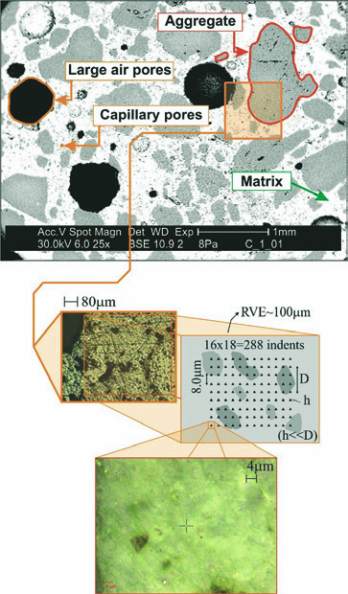
The microstructure of the analyzed composites was split into
two levels. The first level, which corresponds to the matrix level,
named as level I, is characterized by all the matrix phases hav-
ing characteristic dimensions less than
d ≈
10 mm (i.e. hydra-
tion products, clinker, quartz filler, fly ash). The RVE size which
also corresponds to the indentation grid has the dimension
~100 mm. Therefore, the scale separability condition [12,19]
h<<d<<L
, where
h
is the indent size,
d
is the characteristic inclu-
sion size and
L
is the RVE size, holds. The situation is illustrated
in Figure 8.
Since the volume affected by the indentation is ~0.6 mm
3
it is as-
sumed that all the pores smaller than this limit are included in the
indentation results. It includes mainly nanoporosity. However, a
small part of pores with the dimension of 0.6~10 mm, which cor-
responds to approximately 1/10 of RVE size, also lies in the level
I but cannot be detected by the nanoindenter. Consequently, this
porosity was included as an additional mechanical phase in the
level I (Table 7).
Mercury intrusion porosimetry (MIP) performed on the crushed
pieces of the composites of the size of up to 5 mm was used for as-
sessment of the level I porosity, i.e., pores in the range from 0.6 µm
to 10µm, which equaled to 2.4 vol.%, see Figure 9. The results for
the homogenized elastic modulus and the Poisson’s ratio obtained
by the Mori-Tanaka method for level I are presented in Table 7.
Subsequently, the level of the whole mortar, named as level II,
was constructed. It consisted of the homogenized phase of the
level I (matrix) and the rest of components, i.e. large sand par-
ticles, aggregate and air voids, which corresponds to capillary
pores with diameter greater than 10µm and large air voids com-
ing from entrapped air greater than 1mm. Since the aggregate
does not change chemically in the composite, its portion is given
by the initial mixture proportions, defined in Table 3. The elastic
modulus and the Poisson’s ratio of the quartz aggregates were
assumed as 71.8 GPa and 0.17, respectively, [30]. Sometimes,
an additional phase, an interfacial zone between the matrix and
the aggregate, is considered as a separate phase in multiscale
models. For the herein presented analysis, the properties of
possible ITZ are naturally included in the nanoindentation data
since the indentation grid was squeezed between the large ag-
gregate. Moreover, the very dense matrix itself consists of pos-
sibly interconnecting ITZs surrounding the pure phases.
Due to the large span of the pore diameters ranging from mm to
mm, a combination of imaging techniques was used to assess
Figure 8 – Scale definition
Table 7 – Mechanical properties of the level I obtained by homogenization
Phase
Elastic modulus
[GPa]
n
Volume
fraction
[%]
Corrected
volume
fraction [%]
Mori-Tanaka
level-I
E
hom
[GPa]
level-I
hom
n
A
24.4
0.20
6.3
6.2
45.9
0.20
B
41.3
0.20
48.8
47.6
C
54.3
0.20
27.4
26.7
D
81.2
0.20
17.5
17.1
Porosity
–
–
–
2.4

