Basic HTML Version
320
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 3
Contribution to assessing the stiffness reduction of structural elements in the global stability analysis of
precast concrete multi-storey buildings
that not all of the sections in the structural element are made from
materials with values corresponding to lower statistical quantiles.
In other words, not all of the sections in the element are equally af-
fected by the conditions taken into account by coefficient
g
m
, which
considers the weights of strengths.
Regarding the safety of the loads, the second-order analyses were
performed using the M x N x 1/r diagram(s). NBR 6118:2003 [1]
suggests using a formula for safety in which the loads are increased
by
γ
f
/
γ
f3.
After determining the second-order effects, the loads are
increased by
γ
f3
, with
γ
f3
=1.1. According to NBR 8681:2003 [17], the
coefficient
γ
f3
considers the possible errors in evaluating the effects
of the loads, whether from constructive problems or from deficien-
cies in the calculation method used.
Secant stiffness is calculated as follows: a) first, the resistant mo-
ment in the transversal section (M
rd
) is calculated, using a value of
0.85f
cd
for stress on the concrete, and the acting load is increased
by
γ
f
(N
d
); b) next, the M x N x 1/r diagram is constructed using a
value of 1.1f
cd
for stress on the concrete, and the acting load is
increased by
γ
f
/
γ
f3
(N
d
/ γ
f3
). The secant stiffness is defined by the
relationship between the resistant moment(M
rd
)/
γ
f3
and the corre-
sponding curvature in the M x N x 1/r diagram constructed with a
value of 1.1f
cd
of stress on the concrete and acting load increased
by
γ
f
/
γ
f3
(N
d
/
γ
f3
).
The combined effects of the intact concrete between cracks and
the concrete’s tensile strength constitute a phenomenon known as
“tension stiffening”. The manual from fib [18] accounts for this ef-
fect with regard to the relationship M x 1/r. However, this effect is
not taken into account in the present study.
The procedures used here are valid for experimental verifications
of concrete with f
ck
values up to 50 MPa, the maximum strength
grade for which NBR 6118:2003 [1] is applicable. Construction of
the M x N x 1/r diagram is accomplished by determining the axial
strength force (ν
Rd
) that is able to balance a pre-fixed axial force
(ν
fixo
). Because the pre-fixed axial force is associated with a curva-
ture and neutral position, this procedure is necessarily incremental
and iterative. After defining the neutral axis, the dimensionless re-
sistant moment is calculated. The procedure used to construct the
M x N x 1/r diagram and a description of the incremental and itera-
tive process can be found in the study by MARIN [19]. The M x N
x 1/r diagrams can be shown as dimensionless values. The study
of FUSCO [20] details the relationships between the dimension-
less bending moment (µ), the dimensionless axial force (
ν
), and
curvature (d/r) that can be found for different d’/h relationships and
grades of steel. The study of OLIVEIRA [21] contains abacuses
that relate the dimensionless bending moment, the dimensionless
axial force, and the secant stiffness adjusted for the effect of the
linear creep coefficient.
The results obtained in MARIN [19] for the resistant moment and
secant stiffness were compared with the values found in the aba-
cuses developed by OLIVEIRA [20], with differences of approxi-
mately 1%. The values shown in the abaci by FUSCO [20] were
also compared with those obtained by MARIN [19], with differenc-
es of approximately 1%.
4. Numerical simulations in the
representative cases
The analysis herein was performed using a structural arrange-
ment representative of multi-storey precast concrete buildings.
Figure 2 shows the schematic arrangement with modulations of
7.5 m and 10 m.
The structural system used in the present study is constituted by
frames with semi-rigid beam-to-column connections and columns
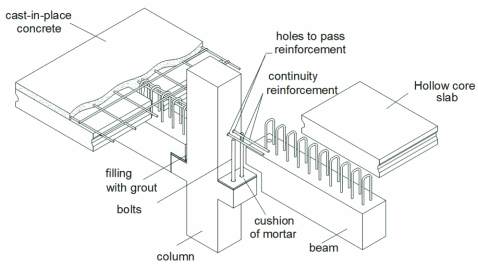
embedded in the foundation. As illustrated in Figure 3, this beam-
to-column connection is formed by two bolts and concrete topping
cast on site, with reinforcement passing through the central col-
umns. On the end columns, the reinforcement for negative bending
moments is anchored in mechanical splices. For any direction in
which there is no column-beam plane, the stability must be en-
sured by the stiffness in the columns. Horizontal wind loads are
transferred to the other components by the slab, which behaves
like a diaphragm. Thus, a central frame in direction y was selected,
as shown in Figure 2, as an object of study.
The semi-rigid behavior of the beam-to-column connection was tak-
en into account using the bending moment x rotation of connection
proposed in El Debs et al. [22], which is reproduced in Figure 4.
Using the semi-rigid beam-to-column connection, the increasing
of floors number typically used with pinned connections (3 floors,
approximately 12 m in height) was investigated. Based on prelimi-
nary calculations, which were subsequently proven, the beam-to-
column connection allowed for increasing the number of floors to 6
when the column’s cross section was 50 cm x 50 cm for a modula-
tion of 7.5 m and 60 cm x 60 cm for a modulation of 10 m. For both
Figure 2 – Schematic arrangement
Figure 3 – Beam-to-column connection

