Basic HTML Version
321
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 3
M. C. MARIN | M. K. EL DEBS
modulations, buildings with up to 4 floors were stable for column
cross-sections of 40 cm x 40 cm.
Based on the above considerations, the variables and parameters
described below were analyzed.
a) Number of floors (height):
4 floors (16 m), 5 floors (20 m), and
6 floors (24 m).
b) Materials:
concrete C-35 (f
ck
=35 MPa), steel CA-50 for longitudinal
reinforcement, and steel CA -60 for cross-sectional reinforcement.
c) Cross-sectional and longitudinal reinforcement in the columns
(according to Table 2): the longitudinal reinforcement (A
s,tot
) was uni-
formly distributed in the sides of the section, and the geometric rate of
reinforcement corresponded to approximately 3% of all the sections of
the columns. The cross-sectional reinforcement consisted of stirrups
with a diameter of 6 mm; and a minimum concrete cover of 2.5 cm for
the cross-sectional reinforcement in the columns was adopted.
d) Dead loads:
the self-weight of the hollow core slab was 2.2 kN/
m
2
for a span of 7.5 m and 2.6 kN/m
2
for a span of 10 m. The struc-
tural concrete topping 6 cm thick, with a self-weight of 1.5 kN/m
2
and a coating of 0.5 kN/m
2
. The average thickness of the structural
concrete topping was 6 cm (considering the upward deflection of
the hollow core slabs);, and, for all cases, a load of 10 kN/m per
floor (resulting from the masonry’s self-weight) was used around
the perimeter of the structure.
e) Live loads:
two values, - 3 and 5 kN/m
2
, were considered.
f) Wind pressure:
wind pressure was calculated according to
NBR 6123:1988 [23]. The force of wind on a given structural ar-
rangement was broken down according to the number of floors and
height, as shown in Table 3, for the case study corresponding to
the central frame with a modulation of 7.5 m.
g) Load combinations:
three load combinations were considered
for ULS: in the first, which employed a high concentration of people
in a typical commercial, public, or office building, the wind’s load
was the main load, and the live load was considered secondary
(this combination was important to verify the global stability of the
structure as a whole). The second combination did not consider
the contribution of the live load (its verification was extremely im-
portant due to the positive moment caused by the wind on connec-
tions). In the third load combination, the live load was predominant,
and the load from the wind was secondary.
Thus, three expressions for load combinations for the ultimate limit
state are obtained, as shown below:
(20)
F
d,1
= γ
g
. G + 1.4(W + 0.7Q)
(21)
F
d,2
= γ
g
. G + 1.4W
(22)
F
d,3
= γ
g
. G + 1.4(0.6W + Q)
where:
G
represents dead loads;
Q
represents live loads;
W
represents wind loads.
The wind load was considered in all combinations; therefore, the
no-bearing walls were finished. The axial force on the columns on
each floor were calculated based on the values of the loads con-
sidered. Table 4 presents the values for all cases for a modulation
of 7.5 m and live load of 3 kN/m
2
.
The axial force is shown in dimensionless form in Table 5. This
form of presentation facilitates the association between the in-
crease in axial force and the increase in the element’s stiffness.
The loads acting on the structure were defined according to each
load combination. Once the loads acting on the structure were de-
fined, the beam and column were characterized with the help of
the M x N x 1/r diagrams, which were built using calculation tools
developed in MARIN [19]. In this way, the strength and stiffness of
the elements were determined.
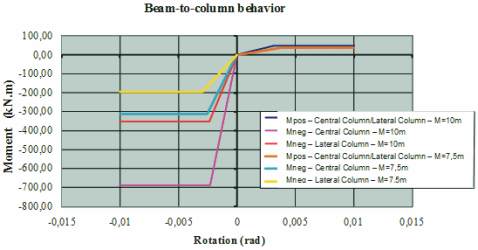
Figure 4 – Bending moment versus rotation curve
Table 2 – Cross sections in the structural arrangements
Cross section (cm x cm)
2
A (cm )
s,tot
M (m)
Nº floors
40x40
50.4 [16
Ф
20 mm]
7.5 e 10
4
50x50
75.6 [24
Ф
20 mm]
7.5
5 e 6
60x60
120.0 [24 25 mm]
Ф
10
5 e 6

