Basic HTML Version
324
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 3
Contribution to assessing the stiffness reduction of structural elements in the global stability analysis of
precast concrete multi-storey buildings
Next, the values found for stiffness reducing according to the M x N
x 1/r diagram were compared with the values obtained from the ap-
proximate functions recommended by standards. Two limiting situa-
tions based on the axial force and the slenderness are considered.
With regard to the axial force, the maximum and minimum axial
force of the load combinations were considered. With regard to the
slenderness, two hypotheses are considered because the beam-to-
column connections studied behave as semi-rigid. In the first, the ef-
fective length of the column corresponded to the difference in height
between floors. In the second, the effective length corresponded to
the maximum value indicated for precast concrete structures with
multiple floors that are unbraced. According to Elliott [24], this value
is at least 2.3 times that of the height difference between floors.
Table 7 presents the reduction coefficients obtained from the rec-
ommendations in the technical literature. The effects of creep on
the columns were not considered. Thus, the creep coefficient
j
=0
in the construction of the M x N x 1/r diagram and in the expression
from FIB [11] are used. Based on the formulas recommended by
ACI 318-08 [10] and PCI [14],
b
d
was 0.
The reduction coefficient recommended by NBR 6118:2003 [1] for
columns is 0.8, while that for beams with symmetric reinforcement
is 0.5. The reduction-coefficient variations depicted in Table 6 indi-
cate no correspondence between the values found herein and the
reduction coefficients suggested for columns in NBR 6118:2003
[1]. Considering that due to the low-level axial force, the behavior
of columns on the 6th floor is very similar to that of beams, the co-
efficient recommended by NBR 6118:2003 [1] can be interpreted
as 0.5. However, with symmetrical reinforcement, the value of the
reduction coefficient determined from the M x N x 1/r diagram is
approximately 0.35.
The reduction coefficient obtained according to NBR 9062:1985
[12] does not agree with the values obtained for the stiffness re-
duction coefficient from the M x N x 1/r diagram, indicating that the
latter is inadequate for the example studied. The values obtained
according to ACI 318-08 [10] correspond well to the intermediate
sections of the column and, when compared to recommenda-
tions from standards, the modulus of elasticity was the same as
NBR 6118:2003 [1].
The procedure presented by PCI [14] and FIB [11] consider the slen-
derness of the column. However, considering the slenderness of the
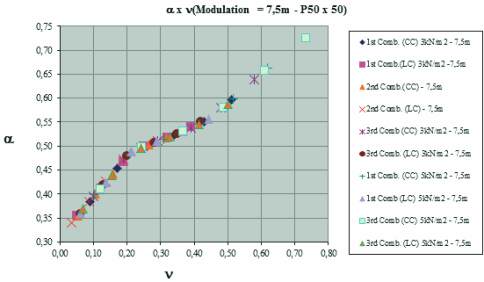
Figure 6 – Diagram of stiffness reduction
coefficient versus dimensionless axial force for
columns (P50x50) in structures with modulation
2
2
of 7,5 m with live load 3 kN/m and 5 kN/m
Figure 7 – Functions for reducing stiffness versus
dimensionless axial force for columns (P50x50)
Table 8 – Functions for reducing stiffness
according to subdomains in dimensionless
axial force for columns (P50x50)
Stiffness reduction function
Subdomain (
n
)
α = 0 .75 ν + 1 .10 (E s I s )/EI
0⩽ ν ⩽ 0.25
α = 0 .46 ν + 1 .32 (E s I s )/EI
0 .25< ν ⩽ 0.75
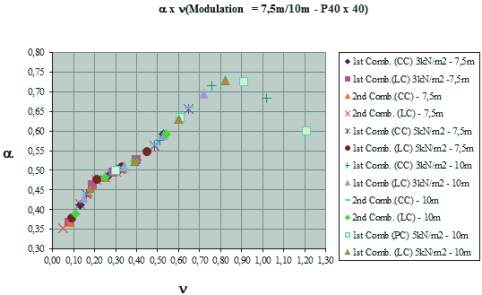
Figure 8 – Diagram of stiffness reduction
coefficient versus dimensionless axial force for
columns (P40x40) in structures with modulation
2
2
(7.5 m;10 m) and live load (3 kN/m ; 5 kN/m )

