Basic HTML Version
325
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 3
M. C. MARIN | M. K. EL DEBS
column makes the analysis more complex because of the semi-rigid
connection and, consequently, the displacement of the structure.
The values obtained for the stiffness reduction coefficient according
to PCI [14] for the two slenderness situations did not agree with the
values obtained from the M x N x 1/r diagram. The values found from
FIB [11] for dimensionless axial force equal to 0.03, were close to
the values found with the M x N x 1/r diagram.
The rate and arrangement of the reinforcement as well as the value
of the axial force have a higher degree of influence in the present
analysis. The analysis of secant stiffness occurs in each section of
the element, and the slenderness of the element is related to the
analysis of the element’s stiffness as a whole.
The study for obtaining stiffness was performed for a structure with
6 floors and live load of 3 kN/m
2
was also done for a live load with
5 kN/m
2
, as observed in the diagram of stiffness reduction coef-
ficients shown in Figure 6. Each data series shown in Figure 6 has
6 points. Each point corresponds to a stiffness reduction coefficient
associated with a floor.
Figure 7 shows two approximations with linear variation divided
into two subdomains. Functions for reducing stiffness according to
the respective sub-domains are proposed, as presented in Table
8. It should be noted with a value of approximately 0.25 for dimen-
sionless axial force, there is a change in the rate of the element’s
increase in stiffness.
The same procedure was performed for columns with cross-sec-
tions of 40 x 40 cm and 60 x 60 cm. This report depicts only the
study designed for the columns with a 40 x 40 cm cross-section
because, in this case, the variation of stiffness decreases upon
reaching a certain level of axial force. Figure 8 shows the variation
in the stiffness reduction coefficient according to the dimension-
less axial force and the modulations and loads to which the col-
umns (40 x 40 cm) were subjected.
In Figure 9, it is possible to evaluate the variation in stiffness
reduction coefficients according to the three subdomains and,
respectively, the three approximate functions. The portion as-
sociated with reinforcement in the reduction stiffness coefficient
has a value of 0.26 when the reinforcement’s area and provision
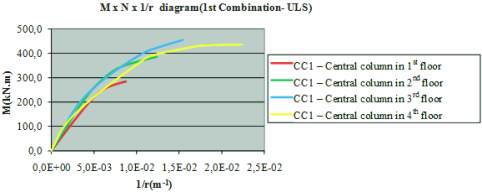
is P(40x40). According to the M x N x 1/r diagram, the reduc-
tion coefficient associated with zero dimensionless axial force is
equal to 0.319.
For the column with a cross-section of 40 x 40 cm, the stiffness de-
creased when the value of the dimensionless axial force reached
0.9. This behavior was not observed for other column sections be-
cause the axial force level was lower. Figure 10 shows the M x
N x 1/r diagram (for the column with a 40 x 40 cm section), which
was constructed with a concrete stress of 1.1 f
cd
and increasing
acting loads by
γ
f
/
γ
f3
(N
d
/
γ
f3
), a modulation of 10 m, and a live load
of 5 kN/m
2
.
Table 9 presents proposed functions for reducing stiffness accord-
ing to respective sub-domains for columns with sections of 40 x
40 cm, 50 x 50 cm, and 60 x 60 cm. Additionally, a function for
reducing average stiffness for each section studied are proposed.
The numerical simulations were designed based on different col-
umn cross-sections, according to the number of floors and the
Figure 9 – Functions for reducing stiffness versus
dimensionless axial force for columns (P40x40)
Figure 10 – M x N x 1/r diagram for first
load combination in central column P40x40
Table 9 – Functions for reducing stiffness according to sub-domains
in dimensionless axial force for columns (P40x40. P50x50. P60x60)
Stiffness reduction function (a)
Cross Section (cm)
0
⩽
n
⩽
0.25
n
0.25 <
⩽
0.85
n
⩽
0.85 < 1.20
40 x 40
0.67ν + 1.15(E
s
I
s
)/EI
0.48ν + 1.20(E
s
I
s
)/EI
–0.24ν + 3.50(E
s
I
s
)/EI
50 x 50
0.75ν + 1.10(E
s
I
s
)/EI
0.46ν + 1.32(E
s
I
s
)/EI
------
60 x 60
0.73ν + 1.12(E
s
I
s
)/EI
0.44ν + 1.29(E
s
I
s
)/EI
------
Avarage value
0.72ν + 1.12(E
s
I
s
)/EI
0.46ν + 1.27(E
s
I
s
)/EI
–0.24ν + 3.50(E
s
I
s
)/EI

