Basic HTML Version
666
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 5
Punching strength of reinforced concrete flat slabs without shear reinforcement
4.3 EUROCODE 2
EUROCODE 2 [8] also bases its recommendations to estimate the
punching resistance of flat slabs in the recommendations of MC90.
Thus, it recommendations are similar to the ones from NBR 6118.
However, this code limits the value of the size effect on
ξ ≤
2.0
and also of the flexural reinforcement ratio
ρ ≤ 2%,
possibly trying
to reduce the trends of unsafe results. Thus, punching strength is
taken as the lowest value provided by Equations 4 and 5. Figure 7b
shows the control perimeters of this code.
(4)
(5)
where:
f
c
is the compressive strength of concrete in MPa (
f
c
≤
90 MPa);
ρ
is the flexural reinforcement ratio of the slab taken as
0, 02
x y
ρ
ρ ρ
= ⋅
≤
;
ρ
x
and
ρ
y
are the flexural reinforcement ratios in or-
thogonal directions x and y, considering only bars wi-
thin a region away
3∙
d
from the faces of column;
200
1
2, 0
d
ξ
= +
≤
;
u
1
is the length of the control perimeter away
2∙
d
of the faces of
column.
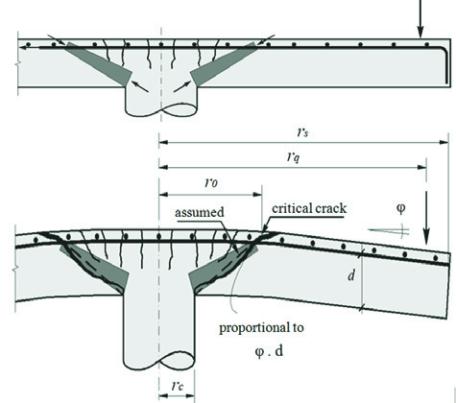
5. Critical Shear Crack Theory (CSCT)
The theory presented by Muttoni [3] is based on the idea that the
punching resistance decreases with increasing rotation of the slab.
This was explained by Muttoni and Schwartz [33] who observed
that the shear strength decreases with the formation of a critical
shear crack that propagates along the slab thickness, cutting the
compression strut responsible for transmitting shear forces to the
column in a mechanism as shown in Figure 8.
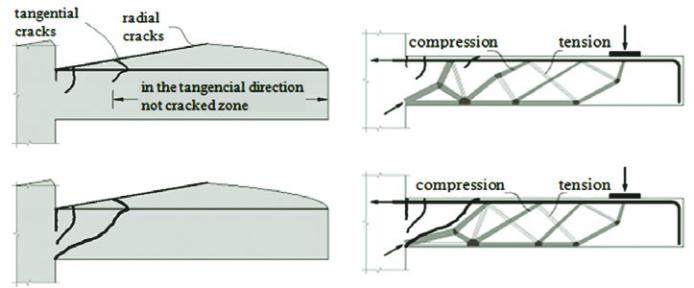
The authors use some experimental evidences to justify this ideali-
Figur� � � �riti��� ����r �r��� t��or�
(Muttoni [3])
Figure � � �tructural beha�ior of slab�column connections after cracking ��uttoni and �ch�art� �����
Cracking in different load stages
Change in strut and tie models
due to cracking of the slab
A
B

