Basic HTML Version
667
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 5
P. V. P. SACRAMENTO | M. P. FERREIRA | D. R. C. OLIVEIRA | G. S. S. A. MELO
zation of the behavior of the slab-column connection. They argue
that, as shown in several experimental punching tests, the curva-
ture in the radial direction is concentrated in the region close to
the support, so that concentric cracks in the form of rings are only
observed in this region. In the rest of the slab only radial cracks
are observed (see Figure 9a). Since shear is not transferred in
the tangential direction, the stress state is not affected by such
cracks. In the region of the tangential cracks, part of the shear
may be resisted by aggregate interlock on the surface of cracks
and another part may be supported by dowel effect of the flexural
reinforcement. As the tensile strength of concrete in the tensile
diagonal is reached the tangential cracks (originally caused by
bending of the slab) start to spread towards the column.
Also according to reports from several authors, including Ferreira
[1], compressive strains in the radial direction nearby the ends of
the column, after reaching a certain maximum value at a certain
load level, start to decrease. Just before the punching failure it is
possible to observe tensile strains in this area. This phenomenon
can be explained by the formation of an elbow shaped strut (see
Figure 9b) with a horizontal tensile member as a result of the ad-
vance of the critical shear crack, cutting the compression zone.
The opening of this crack reduces the resistance of the compres-
sion strut because it affects the capacity of transferring shear for-
ces by interlock aggregate and can eventually lead to a punching
failure. Also according Muttoni and Schwartz [33] the thickness of
this crack is proportional to the product ψ∙
d
(see Figure 8). Howe-
ver, the transmission of shear in the critical crack is directly linked
to its roughness, which in turn is a function of maximum aggregate
size. Based on these concepts Muttoni [3] shows that the shear
strength provided by the concrete can be estimated according to
Equation 6
.
(6)
where:
u
1
is the length of a control perimeter
d
/2
away from the faces of the
column (see Figure 7c);
f
c
is the compressive strength of concrete;
ψ
is the rotation of the slab;
d
g0
is a reference diameter of the aggregate admitted as 16 mm;
d
g
is the maximum diameter of the aggregate used in the concrete
of the slab.
The rotation
ψ
of the slab is expressed by the Equation 7.
(7)
where:
r
s
is the distance between the axis of the column and the line of
contraflexure of moments;
r
q
is the distance between the axis of the column and the load line;
r
c
is the radius of the circular column or the equivalent radius of a
rectangular column;
f
ys
is the yield stress of the tensile flexural reinforcement;
E
s
is the modulus of elasticity of the tensile flexural reinforcement;
V
E
is the applied force;
2
s
flex
R
q c
r
V
m
r r
π
= ⋅ ⋅
⋅
−
;
2
1
2
ys
R
ys
c
f
m f d
f
ρ
ρ
⋅
= ⋅
⋅
⋅ −
⋅
.
With
V
E
, ψ
and
V
R,c
is
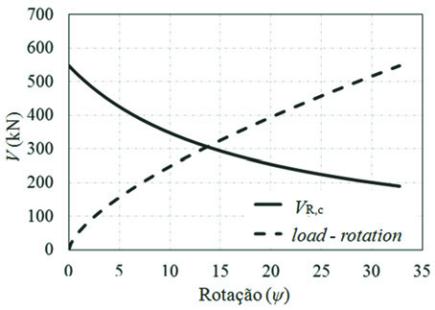
possible to draw a graph with two curves. The
first is a curve that expresses the theoretical load-rotation behavior
of the slab. The second curve expresses the strength reduction of
the slab due to the increase of rotation. The point of intersection of
these two curves express the punching strength of a slab-column
connection. Figure 10 illustrates this graph.
6. Evaluation of theoretical methods
Aiming to evaluate the accuracy of the theoretical methods presen-
ted in the previous sections, results of tests on 74 flat slabs were
taken together in a database. The main criterias for the formation
of this database were the level of reliability of the results, trying to
select results with great acceptance within the scientific community,
and the range of the database related to the parameters that influen-
ce the punching resistance of flat slabs without shear reinforcement.
Were used slabs tested by Elstner and Hognestad [2], Kinunnem
and Nylander [14], Moe [15] Regan [20], Marzouk and Hussein [18],
Tomaszewicz [34] and Hallgren [17]. Table 1 shows the characteris-
tics of the slabs of the database. It should be emphasized that slabs
in this database partially attend the limits of design codes. For exam-
ple, NBR 6118 states that the smallest thickness for a flat slab must
be 160 mm, which does not occur in all the slabs in the database.
However, it is considered that scientifically it is important not to stick
to these limits, since the interest is to understand the phenomenon
as a whole and not just for the most common design situations.
Figure �� � �raphic representation of the punching
strength determination according to CSCT

