Basic HTML Version
583
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 5
R. BARROS | J.S. GIONGO
Similarly, it is observed that the relation between the areas of trans-
verse and longitudinal reinforcement respectively defined by por-
tions T
Rd3
and T
Rd4
with variation of the inclination of the compression
strut present a relation which depends exclusively on the angle of
inclination of the strut. In the case of the transverse reinforcement,
the relation between the areas A
90
depends on the tangent of the
angle θ, and for the longitudinal reinforcement, the relation between
areas A
sℓ
vary according to the cotangent of the angle θ.
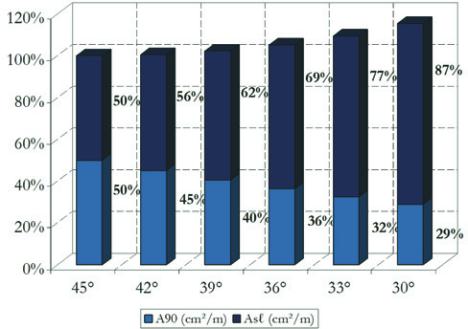
Hence, it is possible to state that as the angle of the strut decrea-
ses from 45° to 30°, there is a gradual decrease in the value of the
transverse reinforcement area A
90
similar to that shown in Figure 2.
By contrast, there is a significant increase in the longitudinal rein-
forcement area A
sℓ
as the strut angle approaches 30°. The greatest
increase occurs when θ equals 30°, in which the longitudinal rein-
forcement area has a 173% higher value than the area obtained
when angle θ equals 45°.
When analyzing the total reinforcement needed to resist torsion, that
is, the combination of the areas obtained for A
90
and A
sℓ
, one obtains
relations between the areas that depend solely on the angle of incli-
nation of the strut. The lowest amount of the total reinforcement is
obtained when angle θ equals 45º, in which the areas of the longi-
tudinal and transverse reinforcement have the same value. As the
angle θ decreases, the increase of the longitudinal reinforcement A
sℓ
is higher than the reduction in the transverse reinforcement A
90,
as
observed in Figure 7. In this situation, there is an increase of 16% in
relation to the total area obtained for an angle of 45°.
4.2 Torsion and shear force effects combined
When the structural element is subjected to the combined effects
of torsion and shear force, some considerations must be made due
to structural safety. The first relates to the adoption of equal incli-
nation angles of the strut, which improves the safety analysis of the
structural element related to torsion and shear force.
The use of the strut angle as less than 45° to the space truss, whi-
ch resists torsion, involves the use of model II for calculating the
shear force. Only when the strut angle is 45 º there is the option
of adopting calculation model I to resist the effects of shear. In
this situation, calculation model II could also be used. However,
as shown in item 3, this consideration leads to elevated values of
transverse reinforcement area because of the shear force.
Another consideration relates to the verification of the strength capa-
city of the compression strut. In this case, independently of the strut
angle and the calculation model considered for the analysis, it is
necessary to attend to the condition expressed in equation (18). This
condition considers the percentage that each action effect requires
to resist the compression strut. It must not exceed 100% because as
it approaches the mentioned ratio, there is a greater chance of rui-
ning the structural element due to rupture of the compression strut.
(18)
1
T
T
V
V
2Rd
sd
2Rd
sd
Regarding the reinforcement area, the principle of superposition of
effects is accepted. That is, the total transverse reinforcement is
given by the sum of the separately design reinforcement for effects
of torsion and shear force, through the portions of A
90
and A
sw
. The
lateral reinforcement A
sℓ
is only calculated if torsion occurs, and it
may be distributed along the equivalent perimeter of the concrete
section, or displayed in the vertices of the section.
As the angle of inclination of the strut varies from 45° to 30°, the
value of the total transverse reinforcement decreases in order that
both A
sw
and A
90
portions also decrease. Thus, the total transverse
reinforcement has its maximum value if calculation model II is con-
sidered, for the shear force, with a 45° angle, and has its minimum
value if the same model is considered, although with an inclination
angle of the strut equal to 30º. The use of calculation model I pro-
vides intermediate values for the total transverse reinforcement.
Figure 8 presents the area of total transverse reinforcement in re-
lation to calculation model I.
Figure � � �ercentage distribution
of torsion reinforcement A e A
90
s
ℓ
Figure � � �otal transverse reinforcement
A e A in relation to reinforcement
90
sw
area from calculation model I
Total transverse reinforcement
0%
20%
40%
60%
80%
100%
120%
45º MII 45º MI
42º
39º
36º
33º
30º
A90+Asw
(A90+Asw),MI

