Basic HTML Version
584
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 5
Shear force and torsion in reinforced concrete beam elements: theoretical analysis based
on Brazilian Standard Code ABNT NBR 6118:2007
At first, the graph in Figure 8 induces the reader to believe that the
situation in which greater reinforcement saving is obtained is the
consideration of calculation model II with the strut angle equal to
30º. However, this conclusion is mistaken due to the existence of
the torsion longitudinal reinforcement A
sℓ
and offset of tensile chord
loads diagram, which was not considered in this study. This rein-
forcement shows higher values as the angle of inclination of the
strut approaches 30°, as shown in Section 4.1. This reinforcement
has to be considered in the total reinforcement design, and then it
is possible to compare calculation models to state which leads to a
lower consumption of the total reinforcement.
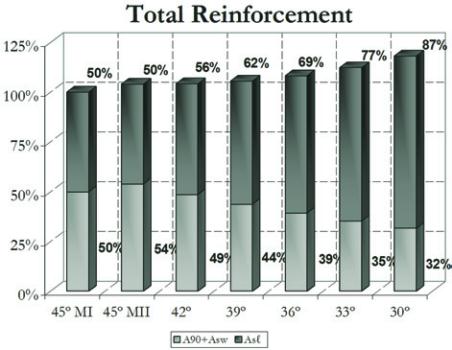
Therefore, the use of calculation model I leads to greater steel sa-
vings when compared to alternatives in calculation model II for con-
sidering angle θ of inclination of the strut. Figure 9 shows the per-
centage distribution of total transverse reinforcement, A
90
and A
sw
,
and torsion longitudinal reinforcement A
sℓ
, in relation to the values
obtained using calculation model I. It is observed that when using
calculation model II with strut angle as 30º, the total reinforcement
presents itself 19% greater than that obtained with calculation model
I. This situation occurs because most of the total reinforcement area
is represented by the torsion longitudinal reinforcement A
sℓ.
5. Conclusion
The analysis of the results of transverse reinforcement areas de-
sign, derived from the isolated action of shear force and torsion as
well as the combined action of these action effects, were presen-
ted. To perform the analysis, vertical stirrups placed at 90º were
considered. Considering the isolated action of the shear force, the
main conclusions are:
n
Calculation model I leads to high values of the transverse rein-
forcement area compared with calculation model II, when using
the strut angle inclined between 30º and 39º. These results are
justified by the fact that calculation model I is a simplification of
calculation model II, therefore, it tends to be more conservative
when considering solely the values of the transverse reinforce-
ment, and not the offset of tensile chord loads diagram effect.
n
In calculation model II, when the strut angle is 45°, one obtains
the same value for design shear resistance V
Rd2
in model I, but
with a greater transverse reinforcement area. If the strut angle
ranges from 40º to 45º, there is a reduction of the values of
V
Rd,2
and A
sw
, but the reinforcement area remains greater than
the one obtained with calculation model I.
n
Based on the results presented, it is not justifiable to use calcu-
lation model II with the strut angle ranging from 40° to 45°.
n
The adoption of the inclination angle of the strut equal to 39° in
calculation model II results in the same area of transverse rein-
forcement obtained when using calculation model I, but with
less strength capacity of the strut.
n
Comparing the results of reinforcement area in calculation mo-
del II in relation to calculation model I, it is observed that the
intensity of the action effects have little influence in the reduc-
tion percentage of the transverse reinforcement area. Howe-
ver, there is little variation in this percentage due to the class of
concrete considered in the design stage.
Regarding the isolated effects of torsion and the combined effects
of torsion and shear force, the following conclusions are presented:
n
The portions of the compression strut, V
Rd2
and T
Rd2,
have equi-
valent reduction as the angle of inclination of the strut decrea-
ses compared with the 45º angle.
n
Regarding the areas of the transverse and longitudinal reinfor-
cement bars derived from the combined action of torsion and
shear force, it appears that as the angle of the strut decreases
from 45° to 30°, there is a reduction of the transverse reinforce-
ment torsion A
90
, an increase in the longitudinal reinforcement
torsion A
sℓ,
and a reduction of the transverse reinforcement due
to shear force, A
sw
.
n
Regarding the percentage distribution of the total transverse
reinforcement area (A
90
and A
sw
), there is a reduction in the
value of the reinforcement areas as the angle θ of the strut de-
creases. For angles of inclination of the strut close to 30º, this
reduction is of approximately 63% in relation to the total area
obtained when the angle is 45°.
n
Concerning the percentage distribution of the total reinforce-
ment area (A
90
, A
sw
and A
sℓ
), there is an increase in the final
value of the reinforcement areas as the angle θ of the strut
decreases, resulting in an approximate 19% increase with an-
gles θ close to 30°, compared to the total area obtained when
considering angle θ equal to 45º.
n
The use of calculation model I for shear force combined with
the effects of torsion leads to greater steel savings when com-
pared to calculation model II.
Finally, it is emphasized that high values of shear force often oc-
cur in transition beams, and usually show high values of bending
moment, which can compromise the design of the longitudinal bars
of the beam. For a beam to present deformations in field 3, it is re-
commended that the design value of shear force does not exceed
40% of the strength capacity value of the compression strut.
6. Acknowledgements
The authors thank the Department of Structural Engineering of
Sao Carlos Engineering School, Universidade de São Paulo, CA-
PES and CNPq for the PhD scholarship of the first author.
Figure 9 � �otal reinforcement A90, A e A
sw s
ℓ
in relation to reinforcement area
from calculation model I

