Page 114 - Riem-Vol6_nº1

108 IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
Numerical-computational analysis of reinforced concrete structures considering the damage,
fracture and failure criterion
ferences can be explained through some factors such as: the model
implemented in this work is unidimensional and it adopts the constitu-
tive relation for the concrete based on the Continuous Damage Me-
chanics; in the work of Jarek et al. [7], in order to simulate the concrete
cracking by evaluating its behavior in relation to the tensile stress, the
Willan-Warnke criterion was used; and for its behavior in relation to
the compression, the von Mises plastification criterion was used.
7.2 Simulation 2
The two-dimensional problem was adapted from Mazars and Pi-
jaudier-Cabot [11]. The problem consists of a reinforced pull rod
with 70 cm in length and rectangular cross-section (10 x 10) cm2,
with a steel bar with moment of inertia I = 490.87 mm4 located in
the centroid of the section (Figure 3). A tensile force P = 23823.53
kN is applied to the free end of the pull rod. It was admitted that the
steel has a non-elastic behavior, which is the same as to suppose
that ks is equal to 1, the value used for εsy being irrelevant.
For the problem discretization, 310 isoparametric linear plane ele-
ments were considered: 270 to simulate the concrete and 31 to
simulate the steel bar. Nine line interface elements were used to
simulate the discontinuity. The modified Newton-Raphson method
combined with the arc-length technique was used in the simula-
tions carried out with this model. The maximum admitted errors at
the end of each load increment were utol = 10-3 and Qtol = 10-3. The
symmetric geometry of the pull rod permitted the modeling of half
of the pull rod. The material parameters are given in Table 2.
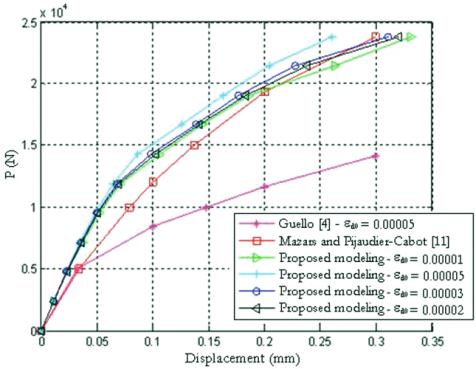
The maximum displacement curves versus load obtained from the pro-
posed modeling by varying the value of εd0, from Mazars and Pijaudier-
Cabot [11] and from Guello [4] are presented in Figure 4. As for the
obtained results, it was verified that the curves obtained from the simu-
lations with the proposed modeling were close to the curve obtained
from the numerical model of Mazars and Pijaudier-Cabot [11].
The crack is simulated through the line interface elements with
linear softening constitutive behavior. The interface parameters
were adopted as per Bessa et al. [2]. Figure 5 shows the maps
of the damage distribution in the concrete that correspond to the
values of εd0 equal to 0.00001, 0.00003 and 0.00005. In all the
cases, it is noticed the formation of new cracks in the transversal
direction to the pull rod and parallel to the existing one, as well
as cracks around the bar. The pulling off the steel bar did not
happen. The variation of the εd0 value causes differences in the
distribution of the damage in the part once the Mazars’ model
predicts the appearance of damage in different spots of the pull
rod for each value.
The cracks that are perpendicular to the part axis will develop if the
tensile stress in the concrete exceeds the tensile stress resistance,
not only around the steel bar but also in the entire cross-section.
These cracks are basically due to the tensile stress from the stress
transference from the steel to the concrete through the adherence.
In fact, in reinforced concrete parts under tensile stress, a relative
sliding always occurs between the armature and the adjacent con-
crete when the strains in both of them have different values. This
sliding occurs mainly due to the crushing of the concrete in front of
the armature bar saliences (Bessa et al. [2]).
Moreover, the contribution of the tangential stiffness component
(Ks ) is disregarded in the constitutive model for simulating the
crack. This simplification may result in singularity and instability in
the numerical analysis once the tangential relative displacement is
without restriction.
8. Conclusions
The traditional analysis of concrete structures is based on labora-
tory tests in structures or structural parts. The results obtained from
these tests are limited and, sometimes, difficult to interpret. Thus,
the development of mathematical-numerical models is needed to
complement the experimental analysis and allow the generaliza-
tion of results for different structures and types of loading.
Figure 3 – Structural model of the reinforced
concrete pull rod with a previous crack
Table 2 – Material parameters
of the structural model
Concrete Steel Interface
E = 30 GPac0
 = 0.2
A = 0.8T
3 B = 5 10T
A = 1.4C
3 B = 2 10C
E = 200 GPaa
 = 0.2
k = 1a
–
– –
– –
-4 G= 4.87 10 kN/cmf
2 K = 0.158 kN/cm0
w = 0.00616 cmc
2 s = 0.158 kN/cmu
Figure 4 – Maximum displacement curve versus load