Basic HTML Version
123
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
R. G. M. de Andrade | L. M. Trautwein | T. N. Bittencourt
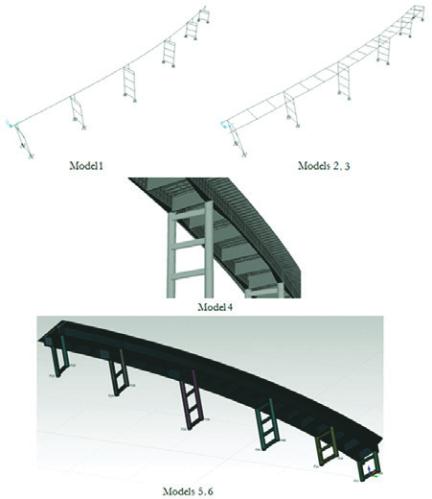
perstructure from the single bar element for two T-shaped girders.
Both girders are connected by the 20 transverse beams.
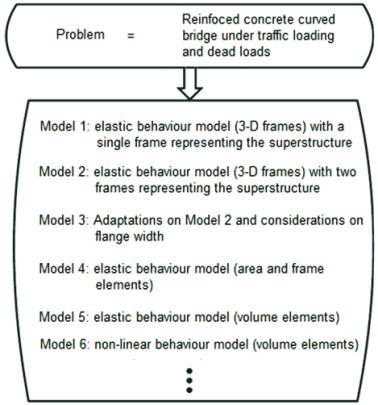
3.2 Model 3
While Model 2 presents the full flange width of the T-shaped sec-
tion, Model 3 shows the same properties and geometric criteria
adopted in modeling, differing by a reduced flange width according
to NBR 6118:2007 (ABNT, [6]).
3.4 Model 4
This model is an enhanced version of the models described above
and uses area elements. However, the columns remain as 3-D
frames. This model allows new considerations to be made, such
as the distribution of the loading on the surface; relative displace-
ment between girders; geometric modeling of transverse beams;
transverse bending of the slab (in relation to the girders). Concrete
properties and the whole structure geometry used to create Model
1 were maintained.
3.5 Model 5
After using area elements in hierarchical model 4, volumetric ele-
ments were used for the development of Model 5 (linear-elastic
behaviour). So far, Model 5 is considered the most complete of the
five described models.
Designed in MIDAS + Fx
software, its geometry was developed
from the insertion of individual points created in Excel spread-
sheets. The software automatically generated the volume ele-
verge. Thus, when changing to a more refined, new hypotheses to
the problem are raised so to reach the final model, to be considered
satisfactory in terms of accuracy and results (Bucalem [5)].
Thus, the physical problem under study is a curved reinforced con-
crete bridge under traffic loads and permanent loads. The possible
numerical models are shown in Figure 2.
The bridge structural analysis over Jaguari river was performed
using numerical models based on the Finite Element Method. Five
linear elastic models were studied and developed, and also a non-
linear model, all using softwares SAP2000 ® V14 (models 1 to 4)
and Midas Fx + for DIANA ® (models 5 and 6). Such models, illus-
trated in Figure 3, will be analysed in order to validate the results
among them.
3.1 Model 1
Model 1 has the advantages for being simple, agile in the creation
and data processing and information in simpler terms of internal
forces. For the whole structure 3-D frame elements were used.
The cross-section of the superstructure was represented as a sin-
gle bar along the whole bridge. Regarding the variation of linear
prismatic cross section of girders, three cross sections were cre-
ated to represent the entire superstructure.
In this model, the entire cross section remains rigid, but with free-
dom for translations and rotations. As the superstructure behaves
like a beam element, the transverse beams were only considered
as dead loading. For the creation of the cross section, the super-
structure superelevation of 8% was taken into account, as well as
the radius of curvature.
3.2 Model 2
Model 2 presents the same geometric and material properties cri-
teria adopted for model 1, except for the replacement of the su-
Figure 2 – Hierarchy of numerical models
for the bridge
Figure 3 – Numerical models (1 to 6)

