Basic HTML Version

124
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
Comparison and calibration of numerical models from monitoring data of a reinforced concrete highway bridge
strength, f
ck
. The adopted equation for E was taken from the Brazil-
ian Standard NBR 6118:2007 [6], shown in Table 1.
The input data for properties and equations for the simulations of
concrete cracking in DIANA are presented in Table 1 (Trautwein
[7]), (Schereppers [8]). It is also presented the equation of the
concrete’s energy of fracture (CEB, [9]). This energy equation is
a function of concrete’s f
ck
and maximum aggregate diameter. It
can be found in DIANA’s library the constitutive model of con-
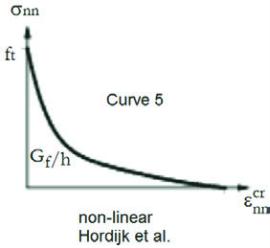
crete’s tensile softening, presented in five different curves. For
this paper, Curve number 5 was adopted, as shown in Figure 5
(Trautwein [7]).
3.8 Boundary conditions
To calculate the stiffness of rubber bearing support, which con-
nects the superstructure with the columns, it was considered
the transverse elastic modulus as G = 1.0 MPa, Poisson’s Coef-
ficient
ν
= 0.5, and durometer Shore A 60. The stiffness coef-
ficients obtained for the spring models 1 to 4 are listed in Table
2 (Braga [10]).
Volume elements for the bearing support were used in models 5
and 6. For both models, a fictitious elastic modulus was adopted
(Braga [10]), as shown in equation 1 below:
(1)
E
fic
= 3G×
[
1+0.5×ν×
(
L e
)
2
]
1-ν
2
The boundary condition for columns support to the ground on all
six models is restriction to the six degrees of freedom – 3 DOF on
translation and 3 DOF on rotation.
3.9 Loadings
In all loading cases, it was considered the structure’s self-weight.
For models 1 to 4, the traffic loading was used according to NBR
6118:2007 (ABNT, [11]) and for models 5 and 6, a real truck loading
was used (truck loaded with gravel). The dimensions and loadings
are shown in Figure 6. For the six models, the traffic loading was
inserted as nodal static loading.
ments, from the insertion of points, drawn lines and areas created
manually for it. Tests were made in order to gain accuracy and a
15cm-sided volume element was chosen.
For this model, the whole structure was modeled into volume elements.
3.6 Model 6
Model 6 has the same geometric description considered in Model
5, differing by the non-linear behaviour of volume elements of su-
perstructure and by inserting concentrations of rebar incorporated
into the concrete mesh (embedded reinforcement).
Figure 4 illustrates all rebar concentrations inserted in the numeri-
cal model; each concentration was placed in the center of gravity of
the represented set. In order to satisfactorily represent concrete’s
non-linearity effects of and cracks’ propagation along the sections
all rebars were strictly included according to the design project.
3.7 Materials properties
The material properties for the input data in the numerical models
were linear-elastic behaviour (models 1 to 5) and non-linear physi-
cal behaviour (Model 6).
The main property so the model can behave elastically is the Elas-
tic Modulus, E, which depends from the concrete’s characteristic
Figure 4 – Rebar concentration for Model 6
Figure 5 – Concrete's tensile softening diagram
(Trautwein [7])

