Basic HTML Version
142
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
The strut-and-tie models in reinforced concrete structures analysed by a numerical technique
due to Eq. [4] in terms of the constitutive matrix can be written in
terms of thickness, due to the direct linear relation between them.
In this context, the performance index in Eq. [7], which takes into
account expression [4] in terms of each thickness and the regulat-
ing function from the SESO procedure, is written as:
(7)
vm
vm
0,max
0,max
0
0 0
vm
vm
i,max
i,max
1
1
σ
σ .
.
PI=
.
=
.
σ
σ .
. . ( )
NE
NE
j j
j j
j
j
A t
A t
A t
A t
j
where
0
t
is the initial thickness and
j
t
is the thickness of the
th
j
element at the ith iteration. The optimal control is obtained by
this performance index, because it is a “monitoring factor” in the
region optimal design. The control for maximizing this parameter
refers to the minimization of the volume control; hence, if the PI
falls markedly, it is a strong indication that it underwent a local
optimum or stationary configuration. However, there is no guar-
antee that this is a global optimum, but a configuration optimal for
engineering design.
5. Numerical examples
Based on the formulation described in previous sections, a com-
puter system was developed applying the SESO in conjunction
with the finite element method, using a linear-elastic formulation for
plane stress state analysis arising from free formulation (Bergan
and Felippa [19]). Thus, some numerical examples are presented
for evaluation and comparison of the configurations obtained by
the classical strut-and-tie models. The optimization parameters RR
and ER, if not mentioned, are equal to 1% and defined as the regu-
latory function
4
10 )(
−
=Γ
η
10
-4
.
5.1 Example 1
In this example discussed by [3], the SESO procedure is applied
to find the best topology for a bridge deck structure subjected to
a uniformly distributed load. The design domain and the boundary
conditions are shown in Figure [3a]. The bridge deck is central and
it represents a region of non-project domain, which means that it
cannot be removed with 180-meter long and 4-meter high dimen-
sions, restricting the elements contained on the board. The uniform
load is applied as concentrated forces, 500 kN per node. The bot-
tom corners of the domain are constrained in the plane, Figure 3a.
The Young´s modulus of the material is E = 200 GPa, the Poisson’s
ratio is 0.30 and the thickness is 300 mm. Figure [3b] shows the
optimal topology obtained by [3], using square finite elements, in-
dicating a well-known “tie-arc” commonly used in the engineering
design of bridges.
Figures [3c] and [3d] show the optimum topology obtained with the
present formulation using a refined mesh with 180x60 elements.
When designing bridge structures, the designer must consider
a number of important aspects such as structural performance,
economy, aesthetic and constructability.
The optimal topology seen in Figure [3c] was obtained due to
boundary conditions applied to the length of the edges of non-de-
sign domain which determines the bridge deck, while the boundary
conditions imposed to achieve the optimal configuration shown in
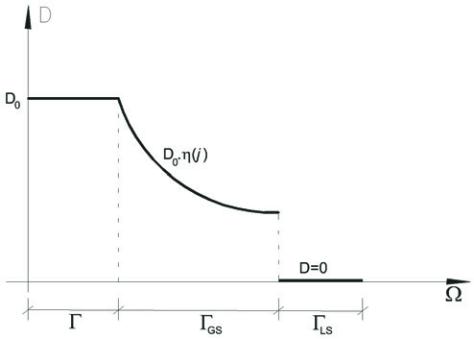
where
GS
LS
Γ+Γ=Γ
LS
+
GS
,
0 ( ) 1
j
η
≤ Γ ≤
is the regulating function that
weights the value of the rate
max
vm vm
e
s
s
within the
Γ
domain, and
this procedure can eliminate the checkerboard problem.
The proposed smoothing can be, for example, performed by
( )
η
Γ
using a linear function of the
( )
j
η
α
β
Γ = +
type or a trigonometric
function of the
( ) sen( )
j
η
α
Γ =
type. Because these two functions
are continuous, they can be differentiated all over of the
Γ
domain,
and they have an image varying from 0 to 1, Figure [2].
4. Performance index for the SESO
formulation
The performance index (PI) is a dimensionless parameter that mea-
sures the structural performance efficiency. The problem consists in
the minimization of the objective function in terms of weight, subject
to an allowable stress constraint (σ
project
), which is defined as:
(5)
b 9
e
e 1
,ma x
minimize W w ( )
subject to
-
0
e
vm
project
j
t
where
NE
is the total number of finite elements. The PI was pro-
posed by Liang
et al
. [5] as:
(6)
0,max
0,max
0,max
0
0 0
0
i,max
i
i,max
i
i,max
i
vm
vm
vm
vm
vm
vm
i
W
V
V
PI
W
V
V
where
0
V
and
i
V
are the initial and
i
th-iteration volumes,
s
0,max
ó
vm
and
s
i,max
ó
vm
are the initial and ith-iteration maximum Von Mises stresses,
and
0
ρ
and
i
ρ
are the initial and ith-iteration densities, which are
equal for an incompressible material. The smoothing generated
Figure 2 – Illustrates the smoothing of the
volume of the elements removed in iteration i

