Basic HTML Version
143
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
V. S. ALMEIDA
|
H. L. SIMONETTI
|
L. OLIVEIRA NETO
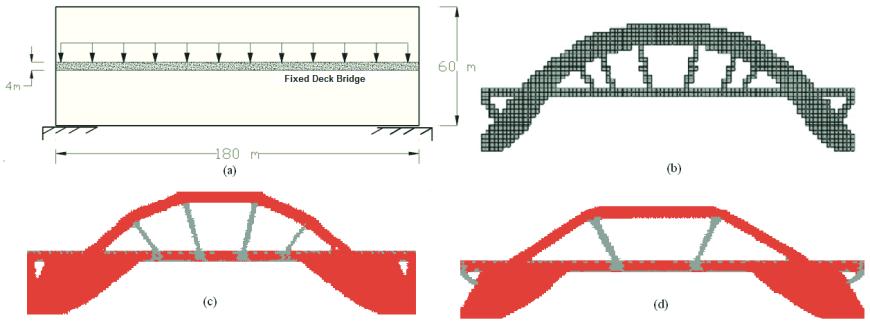
Figure [3d] also includes a constraint on the width of the non-de-
sign domain which represents the bridge deck.
The optimal topology design shown in Figures [3c] and [3d] was
obtained with a final volume of 37.8% and 33.0%, where dark and
light regions respectively indicate the compressed regions, strut,
and tensioned regions, tie.
The optimal settings respectively shown in Figures [3c] and [3d]
were determined with the same optimization parameters, except
for the rejection and the evolutionary ratios. Thus, they were de-
fined as RR =1% and ER = 1.05% in Figure [3c] and RR = 1.1%
and ER = 0.9% in 3d. Note that the proposed algorithm is sensitive
to the variation of these parameters, boundary conditions and the
geometry of the element (Simonetti
et al
., [20]).
5.2 Example 2
The bridge pier shown in Figure [4] is designed to support four
concentrated loads of 2750 kN transferred from four steel-con-
crete composite girders. The bridge pier is clamped on the foun-
dation. An initial thickness of 15 dm is assumed for this bridge
pier. The Young’s modulus is
28600 MPa
E
=
and the Poisson’s
ratio is 0.15.
The optimal topology obtained and the strut-and-tie model pro-
posed by Liang
et al.
[6], which used a method called PBO - Per-
formance-Based Optimization, with 125-mm square, four-node,
plane stress elements. Figure [5a] shows the optimal topology ob-
tained by [6], and Figure [5c] the optimal topology obtained by the
present formulation, SESO, using a refined mesh 170x90, totaling
18,064 triangular finite elements, where the lighter areas represent
the ties. Figure [5b] shows the strut-and-tie model proposed by
[6]. Table [1] shows the efforts obtained by [6] and by the present
formulation for all the members shown in Figures [5b] and [5c]. It
shows a great similarity between the responses obtained by both
procedures with the same arrangement of bars originating from the
strut-and-tie model as well as the efforts obtained at each member
of the bridge pier, which can be designed and detailed following
normative procedures.
Figure [5d] shows the main horizontal reinforcement bars extend-
ed to the extremities in a range of 120 cm. Notes that the sum of
the efforts in ties 1 and 2 is almost the same as that of tie 3. The
vertical components of the efforts in inclined ties are balanced by
vertical reinforcement bars which, as auxiliary reinforcements, are
not displayed in Figure [5d].
5.3 Example 3
This example was reported by Schlaich
et al
. [1]. It is a simply
supported deep beam with a large hole, the geometry and load
(P) of which are presented in Figure [6], which is used as a do-
main extended to the optimization process. The Young’s modulus
is
20820 MPa
E
=
, the Poisson’s ratio is n = 0.15 and the thick-
ness is
0.4
m
. The design strength of reinforced concrete is taken
with values
f
yd
= 434 MPa
and
f
cd
= 25 MPa
. This structure has a
D-region
due to the geometric discontinuity corresponding to the
cavity imposed by the design. In this case, this region should be
evaluated using a strut-and-tie model.
For modeling with the present formulation, 13,200 triangular ele-
Figure 3 – (a) Design domain of the bridge (b), Topology optimal proposed by [3],
(c) and (d) Topology optimal proposed by the present formulation (SESO)
Figure 4 – Design domain of the structure,
[6], measurements in mm

