Basic HTML Version
15
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
P. M. LAZZARI | A. CAMPOS FILHO | F. P. S. L. GASTAL | R. A. BARBIERI | R. C. SCHWINGEL
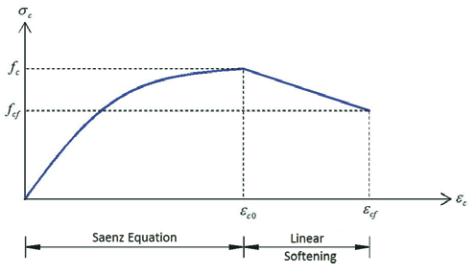
to compressive loads in monotonic loadings, from no strain to
strength peak, as shown in the equation (1) below.
(1)
where:
s
c
: concrete stress;
E
c
: modulus of elasticity of concrete;
e
m
: mechanical strain;
f
c
: compressive strength or peak strength;
e
c0
: strain relative to peak strength.
The softening behavior of concrete after peak strength (
f
c
) is mod-
eled by a stress-linear strain ratio, as shown in equations (2) and
(3), respectively, for concrete stress and tangent modulus of elas-
ticity. The behavior of concrete submitted to compression is shown
on Figure 1.
(2)
c
c
m
t
c
c
f
E
0
(3)
0
c
cf
c
cf
t
c
f
f
E
In concrete submitted to tensile stress in monotonic loadings, the
response is considered linear up to cracking, and the modulus of
elasticity is equal to the initial tangent modulus (
E
c
). When tensile
strength is reached in a section, it is considered that the section
is cracked and that only the reinforcements contribute to tensile
strength forces. However, when there are bonded reinforcements,
concrete also contributes to tensile strength forces, thereby increas-
ing element stiffness in the cracked zone. This behavior is called
eled as additional horizontal planes added to the section. Bonded
reinforcement properties contribute to the element’s stiffness ma-
trix because they are added to section stiffness. On the other hand,
unbonded reinforcements are considered as separate components
acting on the structure. Reinforcement stresses and strains, in-
cluding those of unbonded prestressed reinforcements, are deter-
mined at the element’s integration points.
Relative to composite construction, new integration modules can
be added to sections during analysis, as in the case of slabs cast
on precast beams. In addition, other finite elements can be added
to the structure at any time, simulating the subsequent continuity
of precast members. The parameter time is used to control the
evolution of the building and loading stages, even when the rheo-
logical behavior of materials is not considered in the analysis.
An inclusion date is associated with every structural component,
including section module, finite element, rebar, and prestressing
tendons. Initial and final application dates are also defined for
loading cases. Therefore, at each new loading, the numerical
model compares the initial date of the loading case with the in-
stallation of each structural component, determining which com-
ponents should be considered. In the case of self weight, only
the section parts which inclusion date is the same as the initial
loading date are considered. Also, only the tendons which instal-
lation dates are the same as the initial prestressing step date are
elongated (Barbieri et al, [4]).
2.2 Hybrid finite element formulation
When formulating a hybrid finite element, it is possible to deduce
the stiffness matrix, equivalent nodal load vector, and the element
equation by considering the force interpolation function. During the
analysis, an equation system, consisting of the stiffness matrix and
of the load vector, is assembled and solved, using nodal displace-
ments as unknown factors. These displacements are obtained by
tendon force equilibrium equations. After nodal displacements are
determined, structural node forces are calculated. Responses in-
side the finite element, including stresses, strains, and displace-
ments, are determined by the interpolation of nodal forces (Voelck-
er, [5]).
Hybrid finite element formulation provides a distribution of curva-
tures inside the element bearing a theoretically exact character,
based on the theoretically exact distribution of moments. There-
fore, highly accurate curvature distributions allow the utilization
of long finite elements. In addition, in the case of unbonded pre-
stressed structural elements, the adequate evaluation of curvature
distribution contributes to the correct estimation of prestressed re-
inforcement strains (Barbieri, [2]).
2.3 Material constitutive models
When analyzing the behavior of a structure, the knowledge on the
constitutive equations representing material behavior is essential.
These equations are compatible with the design of the structure;
they model material behavior under predicted loading conditions,
and involve a reduced number of variables in order not to reduce
computational efficiency.
Two different models were used to describe the behavior of con-
crete. Saenz’s equation (Kabaila et al., [6]) was adopted for pre-
stressed concrete. This equation is used for concrete submitted
Figure 1 – Concrete compression behavior

