Basic HTML Version

16
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
Automation of the evaluation of bonded and unbonded prestressed concrete beams, according to brazilian
and french code specifications
(7)
A EB
ps
(8)
0
s
ps
f
E
C
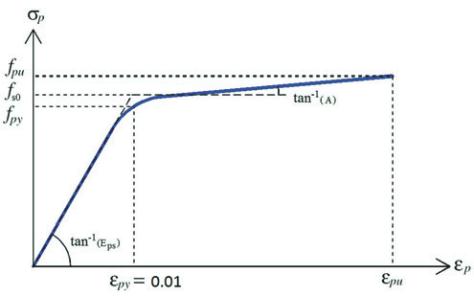
where:
f
py
: conventional yield stress of the prestressing reinforcement
relative to 0.01 strain;
f
s0
: intersection of the tangents of the two linear segments of the
curve.
3. Design criteria
3.1 Brazilian norms
Consistent with the global trend, the Brazilian norm NBR 6118
[10] gathered in a single text the general criteria for the design
of structures made of simple concrete, reinforced concrete, and
prestressed concrete. Depending on the prestressing degree
(complete, limited, or partial), service limit states of decompression
(SLS-D), crack formation (SLS-F), or crack width (SLS-W) are eval-
uated, as well as excessive strain service limit state (SLS-DEF),
and final and prestressing ultimate limit states. Table 1 shows a
summary of the required SLS evaluations for members submitted
to the three prestressing levels, where EEC corresponds to the
environmental exposure class.
Partial prestressing is characterized by a combination of active
and passive reinforcements. In this type of prestressing, tensile
stresses on concrete are allowed to reach higher values, result-
ing in crack widths lower than the limit value recommended by
the norm (
w
k,limite
=
0.2 mm). Table 2 shows the concrete stresses
allowed for each prestressing level. The allowable compressive
tension stiffening, and it is simulated by a slight reduction of concrete
tension stress after stress
f
ct
is exceeded. If this effect is not consid-
ered, displacements are usually overestimated (Ghali & Favre, [7]).
The tension stiffening effect occurs in two intervals: the first presents
higher stress reduction (
b
s
f
ct
) than the second. After an initial drop
in strength, concrete stress gradually decreases at a constant rate
until null value at 0.2% strain is reached. After 0.2% strain, stress and
modulus of elasticity remain null. The above intervals are determined
by parameters
b
and
b
s
,
as shown in Figure 2 (Owen & Figueiras, [8]).
A bi-linear stress-strain curve was used for steel in passive rein-
forcements, where steel bars are represented as an elasto-plastic
material, presenting the same tension and compression behavior.
The curve of Devalapura & Trados [9], shown in Figure 3, was
used for prestressing steel, presenting continuous behavior along
the entire strain interval and no defined yield point. Constants A, B,
and C were obtained from equations (5), (7), and (8), respectively.
Constant D was determined by an iteractive process, solving equa-
tion (4) for yield stress (σ
p
=
f
py
) and strain equal to (
ε
p
=0.01).
(4)
[
]
DD
p
p
p
C
B
A
1
1
where:
ε
p
: strain in the prestressing reinforcement;
σ
p
: stress in the prestressing reinforcement;
A, B, C
and
D
: constants.
(5)
0
0
s
ps
pu
s
pu
ps
f
E
f
f
EA
(6)
py
s
f
f
04.1
0
Figure 2 – Concrete tensile behavior
Figure 3 – Devalapura & Trados [9] stress-
strain relationship, for prestressing steel

