Basic HTML Version
333
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 3
M. C. MARIN | M. K. EL DEBS
6118:2003 [1] descreve duas formas de emprego do diagrama M
x 1/r, a primeira é destinada ao estado limite último e a segunda
para avaliação da rigidez dos elementos. Na Figura 1 é apresenta-
do o diagrama M x 1/r da NBR 6118:2003 [1].
A NBR 6118:2003 [1] prescreve que para efeito de cálculo no ELU
a tensão de compressão de projeto no concreto deve ser mul-
tiplicada por 0,85. Segundo CARVALHO & FIGUEIREDO [15] o
valor de 0,85 f
cd
é atribuído à duração do carregamento no ensaio
do corpo-de-prova, uma vez que o concreto apresenta resultados
de resistência à compressão maior para ensaios de curta dura-
ção. Nas estruturas usuais o carregamento permanece atuando
na estrutura durante toda sua vida útil, sob cargas permanentes
a resistência à compressão do concreto diminui com o tempo, o
chamado efeito Rüsch.
Segundo FRANÇA [16], o cálculo da rigidez obtido a partir das
relações constitutivas baseadas em valores de cálculo da resis-
tência pode conduzir a uma super avaliação dos efeitos da não-
-linearidade. Para efeito de consideração da rigidez a tensão de
compressão de projeto no concreto deve ser multiplicada por 1,10.
A origem deste coeficiente pondera o fato de que nem todas as
seções do elemento estrutural sejam constituídas de material com
valores correspondentes a quantis estatísticos inferiores, isto é,
nem todas as seções ao longo do elemento são igualmente afeta-
das pelas condições que compõe o coeficiente
g
m
, coeficiente de
ponderação das resistências.
Em relação à segurança nas ações, para análises de 2ª ordem
com o auxílio do diagrama M x N x 1/r, a NBR 6118:2003 [1] su-
gere a utilização da formulação de segurança em que as cargas
são majoradas de
γ
f
/
γ
f3 .
Posteriormente à obtenção dos efeitos de
2ª ordem as cargas são majoradas de
γ
f3
, com
γ
f3
=1,1. Segundo a
NBR 8681:2003 [17] o coeficiente
γ
f3
considera os possíveis erros
de avaliação dos efeitos das ações, seja por problemas construti-
vos, seja por deficiência do método de cálculo empregado.
O cálculo da rigidez secante é obtido da forma descrita a seguir:
a) primeiramente é calculado o momento resistente da seção
transversal do elemento (M
rd
), com o valor de 0,85f
cd
de tensão
no concreto e carga atuante majorada de
γ
f
(N
d
) e b) em segui-
da é construído o diagrama M x N x 1/r com o valor de 1,1f
cd
de
tensão no concreto e carga atuante majorada de
γ
f
/
γ
f3
(N
d
/
γ
f3
). A
rigidez secante é definida pela relação entre o momento resistente
(M
rd
)/
γ
f3
e
a correspondente curvatura obtida no diagrama
M x N x 1/r construído com o valor de 1,1f
cd
de tensão no concreto
e carga atuante majorada de
γ
f
/
γ
f3
(N
d
/
γ
f3
).
Em relação à colaboração do concreto íntegro existente entre as
fissuras na capacidade resistente do concreto à tração, conhecida
como “tension stiffening”. A consideração deste efeito na relação
M x 1/r é prevista no manual da fib [18]. No entanto, no presente
trabalho este efeito não foi levado em conta.
As formulações aqui empregadas são válidas até comprovação
experimental para concretos com f
ck
de até 50 MPa, classe de re-
sistência máxima na qual a NBR 6118:2003 [1] é aplicável.
A construção do diagrama M x N x 1/r é feita determinando-se a
força normal resistente (
ν
Rd
) capaz de equilibrar uma força nor-
mal solicitante pré-fixada (
ν
fixo
). Este procedimento é incremental
e iterativo, uma vez que esta força normal solicitante pré-fixada
está associada a uma curvatura e posição de linha neutra. Após a
definição da posição da linha neutra é calculado o momento fletor
adimensional resistente.
O equacionamento para construção dos diagramas M x N x 1/r,
bem como a descrição do processo incremental e iterativo podem
ser encontrados no trabalho de MARIN [19]; neste trabalho foi de-
senvolvida uma ferramenta para construção dos diagramas.
Os diagramas M x N x 1/r podem ser apresentados com valores
adimensionais. Relações momento fletor adimensional (µ) versus
força normal adimensional (ν) e curvatura (d/r), podem ser encon-
tradas para diferentes relações de d’/h e tipos de aço em FUSCO
[20]. Já OLIVEIRA [21] apresenta ábacos que relacionam momen-
to fletor adimensional, força normal adimensional e rigidez secan-
te modificados pelo efeito do coeficiente linear de fluência.
Os resultados obtidos emMARIN [19], de momento fletor resistente e
rigidez secante, foram comparados com os valores encontrados nos
ábacos desenvolvidos por OLIVEIRA [20], apresentando diferenças
da ordem de 1%. Os valores apresentados nos ábacos por FUSCO
[20] também foram comparados com os obtidos por MARIN [19],
apresentando diferenças nos resultados de aproximadamente 1%.
4. Simulação numérica nos casos
representativos
Para fazer a análise foi empregado um arranjo estrutural represen-
tativo de edificações de concreto pré-moldado de múltiplos pavi-
mentos. A Figura 2 mostra a planta esquemática do arranjo, cujas
modulações adotadas foram de 7,5m e 10m.
Figura 2 – Arranjo estrutural estudado
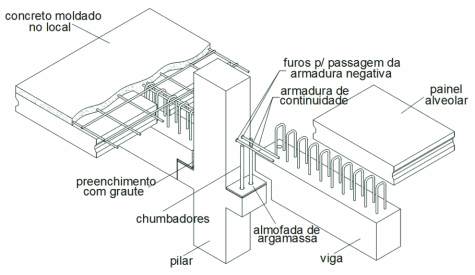
Figura 3 – Ligação viga x pilar semi-rígida
com chumbadores

