Basic HTML Version
594
IBRACON Structures and Materials Journal • 2012 • vol. 5 • nº 5
Shear force and torsion in reinforced concrete beam elements: theoretical analysis based
on Brazilian Standard Code ABNT NBR 6118:2007
na utilização do modelo de cálculo II para força cortante. Apenas
quando o ângulo da biela for considerado igual a 45º, tem-se a
opção de adotar o modelo de cálculo I para resistir aos efeitos
da força cortante. Nessa situação, também poderia ser utilizado
o modelo de cálculo II, entretanto, como apresentado no item 3,
essa consideração conduz a valores elevados para a área de ar-
madura transversal por causa da força cortante.
Outra consideração diz respeito à verificação da capacidade re-
sistente da biela de compressão. Nesse caso, qualquer que seja
o ângulo da biela e o modelo de cálculo considerado para análi-
se, deve-se necessariamente satisfazer a condição expressa na
equação (18). Essa condição considera a porcentagem que de
cada um dos esforços requer de resistência da biela comprimida,
não devendo em hipótese alguma ultrapassar 100% pois, à medi-
da que se aproxima desta relação, indica que há maior probabili-
dade da ocorrência de ruína do elemento estrutural por ruptura do
concreto da diagonal comprimida.
(18)
1
T
T
V
V
2Rd
sd
2Rd
sd
Em relação à área das armaduras, admite-se o principio da su-
perposição dos efeitos. Isto é, a armadura transversal total é dada
pela soma das armaduras calculadas separadamente para os
efeitos de momento torçor e força cortante, por meio das parcelas
de A
90
e A
sw
. No caso da armadura lateral A
sℓ
, é calculada apenas
na situação em que ocorrer torção, podendo ser distribuída ao lon-
go do perímetro equivalente da seção de concreto, ou disposta
nos vértices da seção.
Verifica-se que à medida que o ângulo de inclinação da biela varia
de 45º para 30º, o valor da armadura transversal total diminui, ten-
do em vista que tanto a parcela de A
sw
como a de A
90
diminuem.
Desse modo, a armadura transversal total tem seu valor máximo
caso considere-se o modelo de cálculo II para força cortante com
ângulo igual a 45º, e tem seu valor mínimo caso considere-se o
mesmo modelo com ângulo de inclinação da biela igual a 30º.
Verifica-se que o uso do modelo de cálculo I fornece valores inter-
mediários para armadura transversal total. A Figura 8 apresenta
a área de armadura transversal total em relação ao modelo de
cálculo I.
A princípio, o gráfico da Figura 8 induz o leitor a acreditar que
a situação em que se obtém maior economia de armadura é a
consideração do modelo de cálculo II com ângulo da biela igual a
30º. Entretanto, essa conclusão se mostra equivocada em face da
existência da armadura longitudinal de torção, A
sℓ
e da decalagem
do diagrama de forças no banzo tracionado, que não foi consi-
derado nesse estudo. Verificou-se que esta armadura apresenta
maiores valores à medida que o ângulo de inclinação da biela se
aproxima de 30º, conforme apresentado no item 4.1. Essa arma-
dura precisa ser considerada no cálculo da armadura total, para
então poder comparar qual situação de cálculo conduz a um me-
nor consumo de armadura total.
Verifica-se, portanto, que a utilização do modelo de cálculo I con-
duz a maior economia de aço quando comparadas as alternativas
que se dispõe no modelo de cálculo II para consideração do ân-
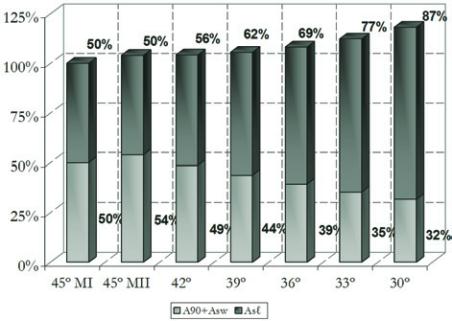
gulo θ de inclinação da biela. A Figura 9 apresenta a distribuição
percentual de armadura transversal total, A
90
e A
sw
, e de armadura
longitudinal de torção A
sℓ
, em relação aos valores obtidos utilizan-
do o modelo de cálculo I. Observa-se que quando da utilização do
modelo de cálculo II com ângulo da biela igual a 30º, a armadura
total apresenta-se 19% maior do que a obtida com o modelo de
cálculo I. Essa situação ocorre em virtude da maior parte da área
total de armadura ser representada pela armadura longitudinal de
torção A
sℓ
.
5. Conclusão
Apresentou-se análise dos resultados dos cálculos das áreas das
armaduras transversais oriundas da ação isolada de força cortante
e momento torçor, bem como da ação conjunta desses esforços.
Em todas as análises consideraram-se estribos verticais dispostos
à 90º. Quando da atuação isolada da força cortante, as principais
conclusões são:
n
O modelo de cálculo I conduz a valores elevados para área de
armadura transversal comparados com o modelo de cálculo II,
quando se utiliza ângulo da biela com inclinação entre 30º e
39º. Esses resultados se justificam em virtude do modelo de
cálculo I ser uma simplificação do modelo de cálculo II, portan-
to, tende a ser mais conservador quando se considera apenas
os valores de armadura transversal, sem considerar o efeito
da decalagem do diagrama de força no banzo tracionado.
n
No modelo de cálculo II, quando utilizado ângulo da biela igual
a 45º, obtém-se o mesmo valor para força cortante resistente
de cálculo V
Rd2
considerando o modelo I, porém com área de
armadura transversal muito maior. Para ângulo da biela situa-
dos entre 40º e 45º, observa-se redução dos valores de V
Rd,2
e
A
sw
, porém a área de armadura continua superior a obtida com
o modelo de cálculo I.
n
Com base nos resultados apresentados, não se justifica utili-
zar o modelo de cálculo II adotando ângulo da biela no interva-
lo de 40º a 45º.
n
A adoção do ângulo de inclinação da biela igual a 39º para
�i�ura � � Armadura total A��� A e A
sw s
ℓ
em relação à área obtida utilizando
o modelo de cálculo I
Armadura total

