Basic HTML Version
117
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
L. A. F. de Souza | R. D. Machado
Onde
n
é o número total de camadas,
b
a largura da seção trans-
versal retangular e
y
i
é a coordenada da i-ésima camada a partir
do centróide da seção. A parcela
EI
eqc
é obtida por:
(32)
EI
eqc
=Σ
i=1
n
E
ci
I
i
Onde
E
ci
=
E
c0i
(1-
D
ji
), com
j
=
C
,
T
, é o módulo de elasticidade lon-
gitudinal do concreto danificado da i-ésima camada. Neste exem-
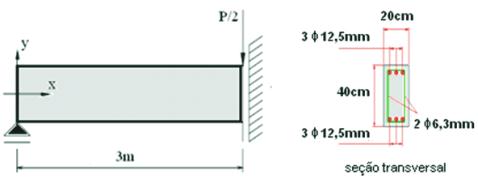
plo, a seção transversal da viga foi dividida em 60 camadas iguais.
A segunda parcela refere-se à rigidez à flexão equivalente para o
aço
EI
eqa
e é determinada pela seguinte expressão:
(33)
EI
eqa
=Σ
k=1
nb
E
ak
(
(
π
Ø
k
4
64
+
π
Ø
k
2
4
y
ai
2
Onde
n
b
é o número de barras;
f
k
o diâmetro da barra
k
;
E
ak
é o módulo
de elasticidade longitudinal do aço da barra
k
; e
y
ai
,
i
= 1, 2, é a distân-
cia do centróide da barra
k
ao centro geométrico da seção transversal
da viga. Assim, a rigidez à flexão equivalente total
EI
eq
é calculada, de
maneira simplificada, pela soma das parcelas
EI
eqc
e
EI
eqa
:
(34)
EI
eq
=EI
eqc
+EI
eqa
Na obtenção do vetor de força interna elementar, a rigidez à flexão
equivalente é determinada para cada ponto de Gauss na integra-
ção numérica, utilizando-se o método de Quadratura Gaussiana.
No processo de cálculo da rigidez equivalente, supõe-se, por sim-
plificação, que a linha neutra (σ
x
= 0) está localizada no centróide
da seção transversal; essa condição é verdadeira desde que haja
simetria da armadura (armaduras longitudinais inferior e superior
com mesma área e posicionadas simetricamente com relação ao
centróide) e os materiais tenham comportamento elástico linear
(lei de Hooke). No entanto, quando os materiais (concreto e/ou
aço) apresentam comportamento não linear, a localização da linha
neutra é alterada. Portanto, em uma análise não linear o posicio-
namento da linha neutra é alterado a cada iteração numérica.
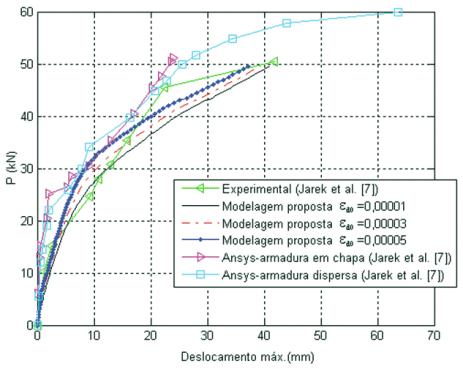
Os resultados obtidos das simulações computacionais com a mo-
delagem proposta variando-se o parâmetro
e
d0
são mostrados na
Figura 2, bem como as curvas numéricas (obtidas com o progra-
ma Ansys) e experimental apresentadas no trabalho de Jarek
et
al
. [7]. Este exemplo evidencia um aspecto importante do modelo
de Mazars que diz respeito à sensibilidade dos resultados quanto
à variação do parâmetro
e
d0
. O dano determinado nos pontos de
Gauss surge no material quando a deformação equivalente atinge
a deformação de referência
e
d0
, ocasionando, assim, a diminuição
da rigidez no ponto correspondente.
Vê-se que, conforme a Figura 2, as respostas numéricas preditas
com a modelagem proposta para a viga são mais rígidas (deslo-
camentos menores) para
e
d0
igual a 0,00003 e 0,00005 até deter-
minado incremento de carga, se comparadas aos experimentais.
Diferentemente, para
e
d0
igual a 0,00001 o deslocamento máximo
v
assume valores numéricos maiores desde o início da análise.
Nota-se também que há uma tendência de comportamento linear,
na relação carga-deslocamento, a partir de certo valor de carga e
se mantém até o processo de ruptura. Segundo os autores Guello
e Bittencourt [5], simulações com o modelo de Mazars podem
conduzir a deformações excessivas na estrutura a partir de um
determinado carregamento. Para limitar essas deformações esses
autores sugerem limitar o valor do dano durante a análise, isto é,
fazer
D
T
< 1 e
D
C
< 1. Contudo, tais restrições não foram consi-
deradas nas simulações realizadas com a modelagem proposta.
Considerando o caso uniaxial de tensão (
σ
1
≠
0,
σ
4
≠
0 e
σ
2
=0), a
Equação (23) é re-escrita da seguinte forma:
(35)
F
1
σ
1
+F
11
σ
1
2
+F
44
σ
4
2
=1
Para todas as simulações efetuadas variando-se
e
d0
, a viga entra
em colapso quando
P
atinge o valor de aproximadamente 50 kN,
ficando próximo à carga de ruptura experimental. No modelo com-
Figura 1 – Modelo estrutural
da viga biapoiada
Figura 2 – Curva deslocamento máximo
versus
incremento de carga

