Page 124 - Riem-Vol6_nº1

118 IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
Numerical-computational analysis of reinforced concrete structures considering the damage,
fracture and failure criterion
putacional, considera-se que a peça falha no momento em que um
dos elementos finitos da malha, em um dos pontos de Gauss, falha,
ou seja, no momento em que a desigualdade F1 σ1+F11 σ1
2+F44 σ4
2 >1
é satisfeita (resultado avaliado a partir da determinação das tensões
máximas na seção transversal correspondente: σ1=σx e σ4=σx/2).
Verificam-se diferenças nas respostas obtidas a partir dos mode-
los tridimensionais (com armadura em chapa e dispersa) com o
auxílio do software Ansys (Jarek et al. [7]) e o implementado neste
artigo. Essas diferenças podem ser explicadas por alguns fatores
como, por exemplo: o modelo implementado neste artigo é unidi-
mensional e adota a relação constitutiva para o concreto baseada
na teoria da Mecânica do Dano Contínuo; já no trabalho de Jarek
et al. [7], para simular a fissuração do concreto, avaliando o seu
comportamento à tração, empregou-se o critério de Willan-War-
nke, e para o comportamento do mesmo à compressão admitiu-se
o critério de plastificação de von Mises.
7.2 Simulação 2
Este problema bi-dimensional foi adaptado de Mazars e Pijaudier-
-Cabot [11]. O problema consiste de um tirante armado de 70 cm
de comprimento e seção transversal retangular (10 x 10) cm2, com
uma barra de aço com momento de inércia I = 490,87 mm 4 loca-
lizada no centróide da seção (Figura 3). Uma força de tração P =
23823,53 kN é aplicada na extremidade livre do tirante. Foi admiti-
do que o comportamento do aço é elástico linear, o que correspon-
de assumir ks igual a 1, sendo irrelevante o valor utilizado para esy.
Para a discretização do problema, foram considerados 310 ele-
mentos planos lineares isoparamétricos: 270 para simular o con-
creto e 31 para simular a barra de aço. Para simular a desconti-
nuidade foram utilizados 9 elementos de interface de linha. Nas
simulações efetuadas com esse modelo, utilizou-se o método de
Newton-Raphson modificado combinado com a técnica de Com-
primento de Arco. Os erros máximos admitidos no final de cada
incremento de carga foram utol = 10 -3 e Qtol = 10-3 . A geometria si-
métrica do tirante permitiu a modelagem de metade do tirante. Os
parâmetros materiais são dados na Tabela 2.
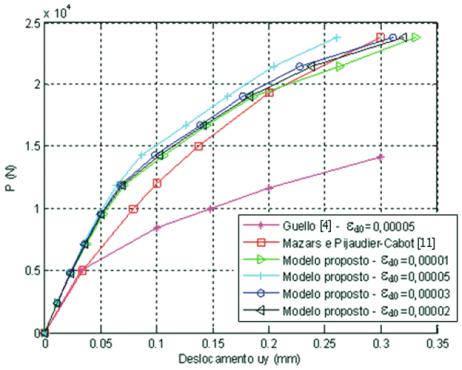
As curvas deslocamento máximo versus carga obtidas da mode-
lagem proposta variando-se o valor de ed0, de Mazars e Pijaudier-
-Cabot [11] e de Guello [4] são apresentadas na Figura 4. Em
relação aos resultados obtidos, verificou-se que as curvas obtidas
das simulações com a modelagem proposta ficaram próximas à
curva obtida do modelo numérico dos autores Mazars e Pijaudier-
-Cabot [11].
A fissura é simulada através de elementos de interface de linha de
comportamento constitutivo de amolecimento linear. Os parâmetros
da interface foram adotados conforme Bessa et al. [2]. Na Figura
5 são mostrados os mapas da distribuição do dano no concreto
correspondentes aos valores de ed0 iguais a 0,00001, 0,00003 e
0,00005. Em todos os casos, nota-se a formação de novas fissuras
transversais ao eixo do tirante e paralelas à existente, bem como
fissuras no entorno da barra. Não houve o arrancamento da barra
de aço. A variação do valor de ed0 ocasiona diferenças na distribui-
ção do dano na peça, uma vez que o modelo de Mazars prediz o
surgimento de dano em pontos diferentes no tirante para cada valor.
As fissuras perpendiculares ao eixo da peça se desenvolvem se a ten-
são no concreto excede a resistência à tração, não somente no entor-
no da barra de aço, mas em toda a seção transversal. Essas fissuras
são, basicamente, devidas à tensão de tração provenientes da transfe-
rência de tensões do aço para o concreto através da aderência.
De fato, em peças tracionadas de concreto armado ocorre um es-
corregamento relativo entre a armadura e o concreto adjacente,
sempre que as deformações de ambos tenham valores diferencia-
dos. Esse escorregamento decorre, principalmente, do esmaga-
mento do concreto em frente às saliências da barra da armadura
(Bessa et al. [2]).
Ademais, no modelo constitutivo para simular a fissura é despre-
zada a contribuição da componente de rigidez tangencial (Ks ).
Essa simplificação pode resultar em singularidades e instabilida-
Figura 3 – Modelo estrutural do tirante
de concreto armado com fissura prévia
Tabela 2 – Parâmetros materiais
do modelo estrutural
Concreto Aço Interface
E = 30 GPac0
 = 0,2
A = 0,8T
3 B = 5 10T
A = 1,4C
3 B = 2 10C
E = 200 GPaa
 = 0,2
k = 1a
–
– –
– –
-4 G= 4,87 10 kN/cmf
2 K = 0,158 kN/cm0
w = 0,00616 cmc
2 s = 0,158 kN/cmu
Figura 4 – Curva deslocamento
máximo versus carga