Basic HTML Version
145
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
V. S. ALMEIDA
|
H. L. SIMONETTI
|
L. OLIVEIRA NETO
spective area, given by the product of beam thickness to the width
of the average flow region.
It is thus possible to calculate the required reinforcement areas in
the tie region and to evaluate the strength of concrete in each strut.
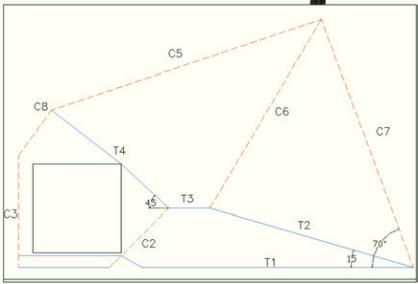
Table [2] shows the values of the average efforts obtained at ties.
The T2 and T4 ties are inclined at 15 and 45 degrees, respectively,
from the horizontal line. The longitudinal bar which represents tie
T2 is calculated from the decomposed horizontal portion of its ef-
forts, thus obtaining the required area of reinforcement As
2
.
Tie T4 has its representation in the orthogonal mesh, As
3
, which
covers the stretch along the edge of the cavity and the in-angle
encounters struts C3, C8 and C5 at the left end. An additional re-
inforcement As
4
, at 45 degrees, is proposed covering the in-angle
encounter struts C2, C5 and C8.
Conforming to the calculation procedures to obtain the representa-
tive reinforcement of ties (Table [2] and Figure [10]), the details of
these reinforcements are shown in Figure [11], where we can see
the proposed extension of reinforcement A
s3
.
Table [3] presents the verification of the compression stresses acting
at strut members where the non-attendance of the ultimate state of
compression in the concrete is observed at struts C3 and C8.
6. Conclusions
Our aim is to present a numerical formulation for the design of
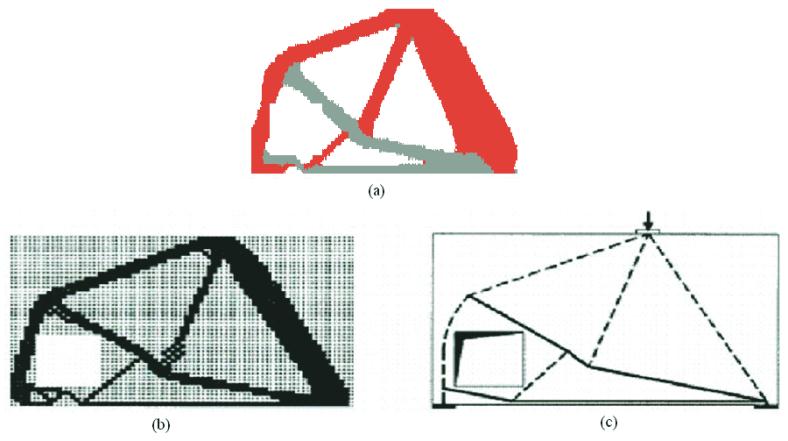
Figure 7 – Optimal topologies obtained by a) the present model;
b) Liang [7], c) Strut-and-tie model proposed by Schlaich et al. [1]
Figure 8 – Performance index versus number
of iterations for the SESO procedure [19]
Figure 9 – Proposed strut-and-tie model

