Basic HTML Version
146
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
The strut-and-tie models in reinforced concrete structures analysed by a numerical technique
reinforced concrete structures under the focus of the strut-and-
tie model.
An alternative topology optimization procedure, called Smooth-
ing Evolutionary Structural Optimization – SESO, was employed
to this end in conjunction with a FEM formulation in stress plane
state analysis. The proposed evolutionary procedure uses a tech-
nique which promotes a “smooth” removal of elements from the
design domain. A priori, an initial extended domain is defined and,
iteratively, the method seeks an optimal topology configuration in
which naturally members are set, indicated by strut-and-tie model.
Thus, the efforts in the members may be evaluated to enable the
design and reinforcement necessary at each section. In contrast
to the ESO method [7], the SESO formulation presents optimal
configurations in the examples, without the side effects of ESO,
such as the “checkerboard” problem, as previously described in
[15] and [20].
Three examples shown demonstrated good accuracy with the
values reported by other authors. A quantification and disposition
of reinforcements were also proposed for a classic example de-
scribed in the international literature on the subject.
7. Acknowledgements
The authors thank the Department of Structural and Geotech-
nical Engineering, Polytechnic School, University of São Paulo
(EPUSP), the University of Ouro Preto (UFOP) and (UNESP) São
Paulo State University for their financial support to this research.
8. References
[01] Schlaich, J; Schafer, K; Jennewe, M. Toward a
consistent design of structural concrete. PCI-Journal,
vol. 32, nr.3, p. 74 – 150, May/June, 1987.
[02] ALI, M. Automatic generation of truss model for the
optimal design of reinforced concrete structures.
Dissertation. Cornell University, Ithaca, NY, USA, 1997.
[03] Liang, Q.Q; Steven, G.P. A performance-based
optimization method for topology design of continuum
structures with mean compliance constraints,
Computer Methods in Applied Mechanics and
Engineering, 191, 13-14, 1471-1489, 2002.
[04] LIANG, Q.Q.; XIE, Y.M., STEVEN, G.P. On equivalent
between stress criterion and stiffness criterion in
evolutionary structural optimization, Structural
Optimization 18,67-13, Springer – Verlag 1999.
[05] Liang, Q.Q.; Xie, Y.M., Steven, G.P. “Topology
optimization of strut-and-tie models in reinforced
concrete structures using an evolutionary procedure”,
ACI Structural Journal, Vol. 97, No. 2, pp. 322-330,
2000.
2
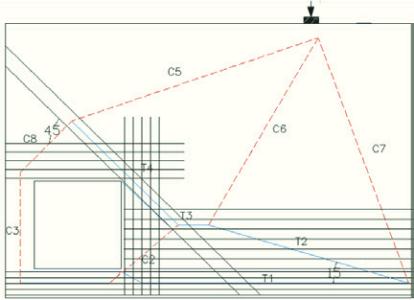
Table 2 – Dimensioning of reinforcement ties (MN, cm )
Ties
Forces (MN)
A
S,nec
2
(cm )
Tie forces
(MN)
Proposed
reinforcement
2
(cm )
Number
of bars
T
1
1.50
34.60
1.50
As = 34.60
1
2 x 5 ø 20
T
2
2.24
51.53
0.966.T
2
As = 49.75
2
2 x 7 ø 20
T auxiliar
4
0.01
–
–
–
–
–
As
4
2 x 2 ø 20
T
4
2.20
50.70
0.707.T
4
As = 35.85
3
2 x 5 ø 20
0.707.T
4
As = 35.85
3
2 x 5 ø 20
Figure 10 – Schematic representation of the
reinforcement bars and strut-and-tie model
using SESO
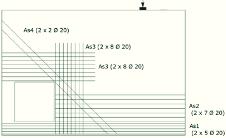
Figure 11 – Proposed disposition of
reinforcement for the present model

