Basic HTML Version
150
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
The strut-and-tie models in reinforced concrete structures analysed by a numerical technique
a qual é definida pra cada elemento finito,
i
i
Γ+Γ=Ω
é o do-
mínio da estrutura, tal que
{ / ( /
( )) RR }
MAX
i
e
VM
i
s s
Γ = Ω
Ω ≥
é o conjunto dos elementos que não serão removidos, e
{ / ( /
( ))<RR }
MAX
i
i
e
VM
i
s s
Γ = Ω − Γ = Ω
Ω
é o conjunto dos ele-
mentos que serão removidos da estrutura (criação do vazio), to-
dos na
i
-ésima iteração.
Na sua heurística de remoção, quando o elemento é removido
do domínio de projeto durante o processo evolucionário, os ele-
mentos que permanecem na estrutura representam uma solu-
ção básica: os termos do vetor gradiente têm valores nulos.
Pois, conforme relatado por Tanskanen [17], pode-se minimizar
a função objetiva escrita em termos da espessura como:
ln[
({ })] ln[ ({ })]
ext
f
W t
V t
=
+
, com
ext
W
sendo o trabalho das
forças externas e V o volume total desta. A derivada parcial da
função objetiva em relação à espessura
t
do elemento
j
fica ex-
pressa por:
(3)
onde
j
A
é a área,
0*
j
W
é a energia média de deformação, todos
do elemento
j,
no total de
m
elementos, e
*0
W
é a energia média
de deformação da estrutura, onde “*” representa o ponto de minimi-
zação ou uma solução básica viável. Em suma, a cada iteração
tem-se uma nova solução básica dentro de uma região viável para
o problema linearizado de OT. Em vista da eq. (3), pode-se afirmar
que o elemento que possui energia média de deformação próxima
da energia de deformação da estrutura tem sua derivada parcial
igual a zero, indicando que um ponto estacionário fora alcançado.
3. Suavização da otimização estrutural
evolucionária (SESO)
Aplica-se sobre o método ESO uma condição de relaxação, ou de
suavização do ESO, apresentando assim um procedimento “soft-
-kill”, de modo que o material, ou seja, os elementos que deveriam
ser removidos pelo critério ESO - seguindo a inequação (1a) - são
organizados em n grupos e alocados em ordem crescente de ten-
sões sendo ponderados segundo uma função
1 )( 0
≤ ≤
j
η
.
Assim, p% destes n grupos são removidos; os grupos que contêm
os elementos com menores tensões (domínio
Γ
LS
), e os grupos
(1-p%) são devolvidos à estrutura (domínio
Γ
GS
). Este processo
de remoção e devolução de elementos à estrutura pode ser orien-
tado por uma função, linear ou hiperbólica, que pondera a razão
MAX
VM
VM
e
dentro do domínio
Γ
, isto é, permite que elementos
que tenham suas tensões próximas e abaixo da tensão máxima,
MAX
VM
, sejam reintegrados à estrutura a cada iteração.
A minimização da função objetiva é atingida mediante o encon-
tro de uma região estacionária, momento em que é alcançado
quando todos os termos do vetor gradiente têm valores nulos, isto
é, se a energía média de deformação do elemento j (
0*
j
W
) tende
para a energia média de deformação da estrutura (
0
j
W
); assim,
o termo (
0*
0*
1
j
W
W
−
) da equação três (3) tende para zero. Deste
modo, entende-se que cada termo do vetor representa um ele-
mento discretizado da estrutura. Tanskanem [17] destaca o fato
forma a incluir as condições de contorno em forças e desloca-
mentos, cavidades e demais condições iniciais. Em um processo
iterativo, avaliam-se os parâmetros de interesse de otimização;
neste artigo em especial é feita a diminuição da massa mediante
um critério de tensão máxima da estrutura. Assim, avaliam-se as
tensões de cada elemento conforme o uso da inequação:
(1a)
(1b)
com
s
vm
e
ó
e
s
vm
max
ó
sendo, respectivamente, as tensão principais
de Von Mises do elemento “e” e máxima da estrutura na iteração
efetiva “ï”; RR é um fator denominado de razão de rejeição.
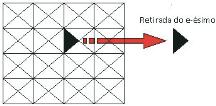
Em cada iteração, os elementos que satisfaçam a inequação (1a)
são retirados da estrutura, figura 1. O fator RR é aplicado para con-
trolar o processo da remoção da estrutura (0,0 ≤ RR ≤ 1,0). O mes-
mo ciclo de remoção dos elementos usados pela desigualdade (1a)
é repetido até que não haja mais elementos que satisfaçam esta
inequação (1a). Quando esta situação ocorre, um estado de equilí-
brio é alcançado. O processo evolucionário é definido adicionando
a
RR
uma razão de evolução (RE). Assim, um novo ciclo de evolu-
ção inicia-se até que não existam mais elementos a serem elimina-
dos com esta nova RR. A RR será atualizada conforme a equação
(1b) até a obtenção de uma configuração otimizada, alcançada pelo
controle de um parâmetro de desempenho, denominado de índice
de performance (IP). Este procedimento também é conhecido como
um método “hard-kill” e pode ser interpretado como segue:
(2)
ﮭ
if j
( )
0 if j
D
D j
�
onde
( )
i
D j
é a matriz constitutiva do elemento
Ω∈
j
na i-
-ésima iteração,
0
D
é a matriz constitutiva inicial do projeto,
Figura 1 – Algoritmo evolucionário: baseado
no elemento removido da malha

