Basic HTML Version
151
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
V. S. ALMEIDA
|
H. L. SIMONETTI
|
L. OLIVEIRA NETO
do tipo
( ) sen( )
j
η
α
Γ =
, porque as duas funções são contínuas e
podem ser diferenciadas em todo o domínio
Γ
e têm sua imagem
variando de 0 a 1, Figura 2.
4. Índice de performance para a
formulação SESO
O índice de performance (IP) é um parâmetro adimensional que
mede a eficiência da performance da estrutura. O problema consis-
te na minimização da função objetiva em termos do peso, sujeito a
uma restrição de tensão admissível (σ
projeto
), que é definida como:
(5)
b 9
e
e 1
,max
minimize W w ( )
sujeito a
-
0
e
vm
project
j
t
onde
NE
é o número total de elementos finitos.
O IP foi proposto por Liang
et al.
[5] como:
(6)
i
vm
i
vm
i
i
vm
i
vm
i
vm
i
vm
V
V
V
V
W
W
IP
0
max ,
max ,0
0 0
max ,
max ,0
0
max ,
max ,0
onde
0
V
and
i
V
são o volume inicial e o volume da i-ésima itera-
ção,
s
0,max
ó
vm
and
s
i,max
ó
vm
são a tensão inicial e a tensão máxima de
Mises na
i
-ésima iteração,
0
ρ
e
i
ρ
são o peso específico inicial
e o peso específico na
i
-ésima iteração, como são iguais para um
material incompressível. A suavização gerada devido à equação
(4) em termos da matriz constitutiva pode ser escrita em termos
de espessura, devido à relação de dependência linear entre elas.
Neste contexto, o IP é representado pela equação (7), que leva
em conta a expressão (4) em termos de espessura e cada função
reguladora do procedimento SESO:
(7)
NE
j
j
j
vm
i
vm
NE
j
j
j
vm
i
vm
j
tA
tA
tA
tA
IP
1
0 0
max ,
max ,0
1
0 0
max ,
max ,0
)(
onde
0
t
é a espessura inicial e
j
t
é a espessura do elemento na
iteração
j
. O controle do ótimo é feito por este fator IP, fator de
“monitoramento” da região ótima de projeto. O controle da maxi-
mização deste parâmetro refere-se ao controle de minimização do
volume; assim, caso este índice mude de forma acentuada é uma
forte indicação que passou por uma configuração ótima ou um
ótimo estacionário foi alcançado; no entanto, não se pode garantir
que este ótimo é um ótimo global, mas sim uma configuração óti-
ma de projeto de engenharia.
5. Exemplos numéricos
De posse da formulação descrita nos itens anteriores, desenvol-
veu-se um sistema computacional aplicando o SESO em conjun-
to com o método dos elementos finitos, usando uma formulação
de que a retirada de um elemento pode afetar a convergência do
procedimento de otimização, pois o critério de retirada no ESO
é indicado pelo atendimento da inequação (1a), que muitas ve-
zes pode ser radical. Podem existir elementos que estão na vi-
zinhança da esquerda dessa condição que numericamente são
excluídos, mas têm uma energia de deformação equivalente a da
estrutura e deveriam compor o vetor gradiente que define ponto
estacionário citado por Tanskanem [17]. A retirada de um elemento
indevidamente pode afetar o caminho do ótimo. Uma forma de
corrigir esse desvio seria a possibilidade de inserção do elemento
na estrutura novamente, destacando que nesse sentido tem-se
uma variante do ESO, o BESO - Bidirectional ESO, Querin [18],
que possibilita a entrada e remoção de elementos no domínio de
projeto. O SESO vem dessa filosofia e, de forma consistente ma-
tematicamente, pondera a matriz constitutiva fazendo a energia de
deformação deste elemento aumentar e tendendo para a energia
de deformação da estrutura; em seguida, o gradiente tende a zero
e a direção do mínimo é restaurada.
Os elementos que estão próximos ao limite pela esquerda des-
ta tensão máxima são mantidos na estrutura, definindo assim um
procedimento de retirada “não radical” e de forma suave. O pro-
cedimento “soft-kill” usado no SESO pode ser interpretado assim:
(4)
LS
GS
j
i
i
j se
j se
D
j seD
jD
0
) (
)(
0
0
onde
GS
LS
é o domínio dos elementos que atendem à
inequação (1a),
iLS
é o domínio dos elementos que devem ser
excluídos efetivamente,
iGS
o domínio dos elementos que são
devolvidos à estrutura,
0 ( ) 1
η
≤ Γ ≤
é uma função reguladora que
pondera o valor da razão
MAX
VM
VM
e
dentro do domínio
Γ
.
A proposta da suavização pode ser desempenhada por uma fun-
ção linear do tipo
( )
η
α
β
Γ = +
ou uma função trigonométrica
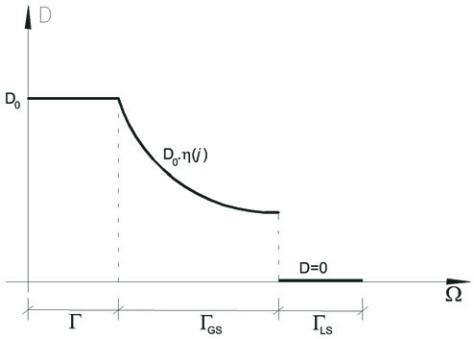
Figura 2 – Ilustração da suavização do volume
dos elementos removidos na iteração i

