Basic HTML Version
152
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
The strut-and-tie models in reinforced concrete structures analysed by a numerical technique
elástica-linear em estado plano de tensões, com o elemento finito
advindo da formulação livre, baseado em Bergan e Felippa [19].
Assim, apresentam-se resultados numéricos para a avaliação e
comparação das configurações obtidas pelo modelo clássico de
bielas e tirantes. Nos desenhos, as regiões mais escuras repre-
sentam os trechos de bielas e as mais claras de tirantes. Os parâ-
metros de otimização RR e RE, quando não citados, são iguais a
1% e a função reguladora definida como
4
10 )(
.
5.1 Exemplo 1
Neste exemplo discutido por [3], a técnica SESO é usada para en-
contrar a topologia ótima de uma estrutura de ponte com tabuleiro
central e sujeita a um carregamento uniformemente distribuído. O
domínio de projeto e as condições de contorno estão ilustrados na
Figura 3a. O tabuleiro da ponte é central e representa uma região
que não pode ser retirada, de dimensões de 180 metros de compri-
mento por 4 metros de altura, restringindo-se os elementos contidos
no tabuleiro e aplicando o carregamento uniformemente distribuído
como forças concentradas de 500 kN por nó. Os cantos inferiores
do domínio são restringidos no plano, figura 3a. O módulo de elas-
ticidade do material é
200 Pa
E G
=
, o coeficiente de Poisson de
0,30 e espessura de 300 mm. A Figura 3b mostra a topologia ótima
obtida por [3], usando elementos finitos quadrangulares, indica um
conhecido “tie-arc” comumente utilizados nos projetos de engenha-
ria de pontes. As Figuras 3c e 3d mostram a topologia ótima obtida
com a presente formulação usando uma malha refinada de 180x60
elementos, onde os trechos mais claros são os tracionados, tiran-
tes. No projeto de estrutura de pontes o projetista deve considerar
uma série de aspectos importantes, tais como: estruturais, desem-
penho, econômico, estético e a constructibilidade.
A topologia ótima encontrada na Figura 3c foi devido a condições
de contorno aplicada no comprimento das arestas do não-domínio
de projeto, que determina o tabuleiro da ponte, enquanto as condi-
ções de contorno impostas para conseguir a configuração ótima é
mostrada na Figura 3d, que também inclui uma restrição na largu-
ra do não-domínio de projeto que representa o tabuleiro da ponte.
As topologias ótimas mostradas nas Figuras 3c e 3d foram obtidas
com um volume final de 37,8% e 33,0%, onde as regiões escu-
ras e claras, indicam, respectivamente, as bielas e os tirantes. As
configurações ótimas mostradas nas Figuras 3c e 3d, respectiva-
mente, foram determinadas com iguais parâmetros de otimização
iguais exceto para a razão de rejeição e a razão evolucionária,
definidas respectivamente como RR =1% e RE = 1,05% (Figura
3c) e RR = 1,1% e RE = 0,9% (Figura 3d). Nota-se que o algoritmo
proposto é sensível à variação destes parâmetros, das condições
de contorno e da geometria do elemento (Simonetti
et al.
[20]).
5.2 Exemplo 2
A Figura 4 mostra um pilar de ponte projetado para suportar quatro
cargas concentradas de 2,75 MN transferidas por quatro vigas de
aço-concreto. O pilar de ponte é fixado na fundação. Uma espes-
sura 1,5m é assumida para este pilar de ponte. O módulo de elas-
ticidade é de
28600 MPa
E
=
, o coeficiente de Poisson de 0,15.
A melhor topologia obtida é o modelo de bielas e tirantes propos-
tos por Liang
et al.
[6], que usou um método denominado PBO
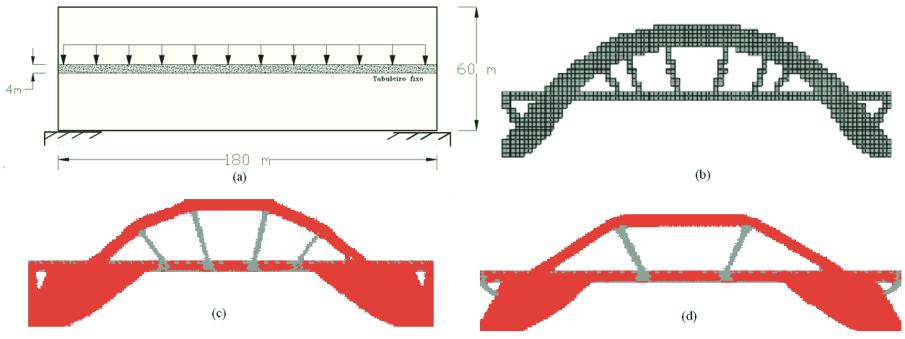
Figura 3 – (a) Domínio de projeto da ponte (b), Topologia ótima proposta por [3],
(c) e (d) Topologias ótimas obtidas com a presente formulação (SESO)
Figura 4 – Domínio de projeto da
ponte, [6], medidas em mm

