Basic HTML Version
36
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
Automation of the evaluation of bonded and unbonded prestressed concrete beams, according to brazilian
and french code specifications
2.3 Modelos constitutivos dos materiais
Para a análise do comportamento de uma estrutura, é essencial o
conhecimento das equações constitutivas que representam o com-
portamento dos materiais. Elas são compatíveis com a idealização da
estrutura, modelam o comportamento dos materiais nas condições
de carregamento previsto e envolvem um número reduzido de variá-
veis, de forma a não prejudicar a eficiência computacional.
Em relação ao concreto, foram utilizados dois modelos diferentes para
descrever o seu comportamento. Para o concreto comprimido foi adotada
a equação de Saenz (Kabaila et Al, [6]), que é utilizada para o concreto
sob cargas de compressão em carregamentos monotônicos, desde a de-
formação nula até o pico de resistência, conforme indica a equação (1).
(1)
Onde:
s
c
: tensão no concreto;
E
c
: módulo de elasticidade do concreto;
e
m
: deformação mecânica;
f
c
: resistência à compressão ou resistência de pico;
e
c0
: deformação relativa ao pico de resistência.
O comportamento de amolecimento do concreto após o pico de re-
sistência (
f
c
) é modelado por uma relação tensão-deformação line-
ar, como mostrado nas equações (2) e (3), respectivamente, para a
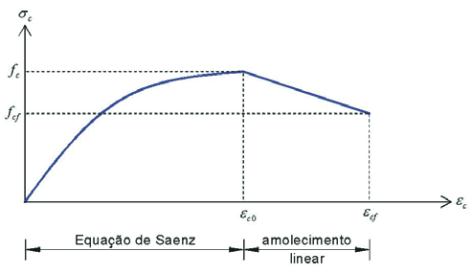
tensão e o módulo de elasticidade tangente do concreto. O compor-
tamento do concreto à compressão pode ser observado na figura 1.
(2)
c
c
m
t
c
c
f
E
0
(3)
0
c
cf
c
cf
t
c
f
f
E
transversal em qualquer ponto arbitrário, situado ao longo do eixo
vertical, não necessariamente no baricentro da seção.
Assim como os módulos de integração do elemento, existem tam-
bém os módulos de integração da seção, os quais são utilizados
como subintervalos com propriedades homogêneas, a fim de re-
presentar descontinuidades ao longo do eixo de integração. Varia-
ções bruscas nas larguras das lâminas, como nos casos das se-
ções I ou T, ou partes da seção com diferentes concretos, comuns
em vigas e lajes, são alguns exemplos de descontinuidade que
podem ocorrer ao longo do eixo vertical das seções.
As armaduras passivas e ativas, aderentes ou não aderentes, são
modeladas como lâminas adicionais incorporadas à seção. As
propriedades das armaduras aderentes contribuem para a matriz
de rigidez do elemento, pois são somadas à rigidez das seções. Já
as armaduras não aderentes, são consideradas como componen-
tes separados que atuam sobre a estrutura. As tensões e defor-
mações das armaduras, inclusive as de protensão não aderentes,
são determinadas nos pontos de integração do elemento.
Em relação à construção composta, as seções podem receber novos
módulos de integração ao longo da análise, como, por exemplo, em la-
jes moldadas sobre vigas pré-moldadas. Além disso, outros elementos
finitos podem ser adicionados à estrutura em qualquer instante, simu-
lando a continuidade posterior de peças pré-moldadas. A variável de
tempo é utilizada para o controle da evolução das etapas construtivas e
de carregamento, mesmo em análises onde o comportamento reológi-
co dos materiais não é considerado. A cada componente da estrutura,
seja módulo de seção, elemento finito, barra de armadura ou cabo de
protensão, é associada uma data de inclusão. Para os casos de car-
ga, também são definidas datas iniciais e finais de aplicação. Assim, a
cada novo carregamento, o modelo numérico compara a data inicial do
caso de carga com a data de instalação de cada um dos componentes
da estrutura, verificando quais devem ser considerados. No caso do
peso próprio, apenas as partes da seção cuja data de inclusão coincide
com a data inicial do carregamento são consideradas. Da mesma for-
ma, apenas os cabos cujas datas de instalação são iguais ao de início
da etapa de protensão são alongados (Barbieri et al, [4]).
2.2 Formulação do elemento finito tipo híbrido
Na formulação do elemento finito do tipo híbrido, a matriz de rigidez,
o vetor de cargas nodais equivalentes e a equação do elemento
podem ser deduzidos considerando-se a função de interpolação de
forças. Durante uma análise, o sistema de equações, constituído
pela matriz de rigidez e pelo vetor de cargas, é montado e resolvido,
tendo como incógnitas os deslocamentos nodais. Estes desloca-
mentos são obtidos através da utilização das equações de equilíbrio
de forças nas barras. Uma vez determinados os deslocamentos no-
dais, são calculados os esforços nos nós da estrutura. As respostas
no interior do elemento finito, incluindo solicitações, deformações e
deslocamentos, são determinadas a partir da interpolação das for-
ças nodais (Voelcker, [5]).
A formulação do elemento finito do tipo híbrido fornece uma distri-
buição de curvaturas no interior do elemento de caráter teoricamen-
te exato, a partir da distribuição teoricamente exata de momentos.
Desta forma, as distribuições de curvaturas de elevada precisão per-
mitem a utilização de elementos finitos longos. Além disto, no caso
de elementos estruturais com protensão não aderente, a adequada
avaliação da distribuição de curvaturas contribui para a correta esti-
mativa das deformações nas armaduras de protensão (Barbieri, [2]).
Figura 1 – Comportamento do concreto
à compressão

