Basic HTML Version
37
IBRACON Structures and Materials Journal • 2013 • vol. 6 • nº 1
P. M. LAZZARI | A. CAMPOS FILHO | F. P. S. L. GASTAL | R. A. BARBIERI | R. C. SCHWINGEL
s
p
: tensão na armadura de protensão;
A, B, C
e
D
: constantes.
(5)
0
0
s
ps
pu
s
pu
ps
f
E
f
f
EA
(6)
py
s
f
f
04,1
0
(7)
A EB
ps
(8)
0
s
ps
f
E
C
Onde:
f
py
: tensão convencional de escoamento da armadura de proten-
são, relativa a uma deformação de 0,01;
f
s0
: intersecção das tangentes dos dois segmentos lineares da curva.
3. Critérios de projeto
3.1 Normalização brasileira
Acompanhando uma tendência mundial, a norma brasileira NBR
6118 [10] reuniu em um só texto os critérios gerais que regem
o projeto das estruturas de concreto simples, de concreto arma-
do e de concreto protendido. Dependendo do grau de protensão
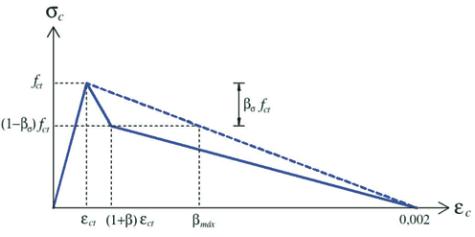
Para o concreto submetido a tensões de tração em carregamen-
tos monotônicos, a resposta é considerada linear até a fissura-
ção, sendo o módulo de elasticidade igual ao módulo tangente
inicial (
E
c
). Se a resistência à tração é atingida em uma seção,
considera-se esta seção fissurada, e que apenas as armaduras
contribuem para a resistência aos esforços de tração. No entanto,
quando existem armaduras aderentes, o concreto também contri-
bui para resistir aos esforços de tração, aumentando, dessa forma,
a rigidez do elemento na zona fissurada. Este comportamento é
chamado de
tension stiffening
e é simulado por meio de uma re-
dução suave na tensão de tração do concreto, após exceder a
tensão
f
ct
. A desconsideração deste efeito normalmente resulta em
uma avaliação exagerada dos deslocamentos (Ghali & Favre, [7]).
O efeito
tension stiffening
ocorre em dois intervalos, sendo que o
primeiro apresenta uma redução de tensão (
b
s
f
ct
) mais acentuada
e o segundo, mais suave. Após a queda inicial na resistência, a
tensão no concreto decresce gradativamente a uma taxa constan-
te até atingir um valor nulo a uma deformação de 0,2 %. A partir da
deformação de 0,2 %, a tensão e o módulo de elasticidade perma-
necem nulos. Os intervalos acima são governados pelos parâme-
tros
b
e
b
s
,
conforme mostrado na figura 2 (Owen & Figueiras, [8]).
Foi utilizada a relação tensão-deformação bi-linear para o aço das
armaduras passivas, onde as barras de aço são representadas
como um material elasto-plástico e apresentam o mesmo compor-
tamento em tração e compressão.
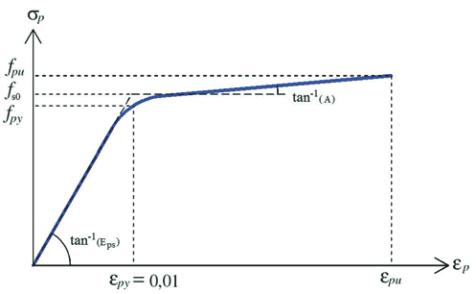
Para o aço de protensão, foi utilizada a curva de Devalapura & Trados
[9], indicada na figura 3, que mostra um comportamento contínuo ao
longo de todo o intervalo de deformações, semapresentar umponto de
escoamento definido. As constantes A, B e C são obtidas a partir das
expressões (5), (7) e (8), respectivamente. A determinação da constan-
te
D
ocorre por um processo iterativo, resolvendo a equação (4) para
a tensão de escoamento (σ
p
=
f
py
) e a deformação igual à (
ε
p
=0,01).
(4)
[
]
DD
p
p
p
C
B
A
1
1
Onde:
e
p
: deformação na armadura de protensão;
Figura 2 – Comportamento do concreto à tração
Figura 3 – Curva de Devalapura & Trados [9]
para o aço de protensão

